题目内容
7.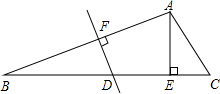 如图,△ABC中,∠C=60°,AB的垂直平分线交BC于点D,DE=6,BD=6$\sqrt{2}$,AE⊥BC于E,求EC的长.
如图,△ABC中,∠C=60°,AB的垂直平分线交BC于点D,DE=6,BD=6$\sqrt{2}$,AE⊥BC于E,求EC的长.
分析 首先作出辅助线连接AD,再利用线段垂直平分线的性质计算.
解答 解:连接AD,
∵AB的垂直平分线交BC于点D,
∴BD=AD,
∵DE=6,BD=6$\sqrt{2}$,
∴AD=6$\sqrt{2}$,
∴∠ADE=45°,
∴∠B=22.5°,∵∠C=60°,
∴∠BAC=97.5°,
∵∠ADE=∠B+∠DAB=45°,AE⊥BC,
∴DE=AE=6,
∵∠C=60°,
∴∠CAE=90°-60°=30°,
∴AC=2CE,
在Rt△ACE中,AC2=AE2+CE2,
即4CE2=62+CE2,
∴CE2=12,
解得EC=2$\sqrt{3}$.
点评 本题考查了线段垂直平分线的性质,解直角三角形,本题关键是作出辅助线提示:连接AD.考查的是线段垂直平分线的性质(垂直平分线上任意一点,和线段两端点的距离相等)有关知识.

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目
15.多项式$\frac{1}{2}$x|m|-(m-2)x+7是关于x的二次三项式,则m的值为( )
| A. | 2 | B. | -2 | C. | ±2 | D. | 3 |
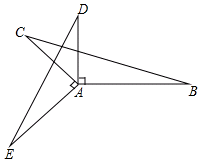 已知:∠EAC=∠DAB=90°,AB=AE,AC=AD,求证:∠E=∠B.
已知:∠EAC=∠DAB=90°,AB=AE,AC=AD,求证:∠E=∠B.
 在△ABC中,点D是BC上一点,F是BA延长线一点,DF交AC于E,∠B=42°,∠C=59°,∠DEC=47°.求∠F.
在△ABC中,点D是BC上一点,F是BA延长线一点,DF交AC于E,∠B=42°,∠C=59°,∠DEC=47°.求∠F.