题目内容
3.在平面直角坐标系xOy中,直线y=$\frac{1}{2}$x+b与双曲线y=$\frac{6}{x}$的一个交点为A(m,3).(1)求m和b的值;
(2)过A的直线交双曲线于另一点B,交x轴于点C,若AC=3BC,请直接写出点B的坐标.
分析 (1)利用待定系数法即可解决问题.
(2)分两种情形①当点B在第四象限时,作AE⊥x轴于E,BF⊥x轴于F,由AE∥BF,得到$\frac{AE}{BF}$=$\frac{AC}{BC}$=$\frac{3}{1}$,推出BF=1,②当点B在第一象限时,作AE⊥x轴于E,BF⊥x轴于F,由AE∥BF,得$\frac{AE}{BF}$=$\frac{AC}{BC}$=$\frac{3}{1}$,推出BF=1,由此即可解决问题.
解答 解:(1)把点A(m,3)的再把代入y=$\frac{6}{x}$得到m=2,
再把A(2,3)的再把代入y=$\frac{1}{2}$x+b,3=1+b,解得b=2,
所以m=2,b=2.
(2)如图,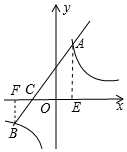
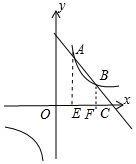
①当点B在第四象限时,作AE⊥x轴于E,BF⊥x轴于F,
∵AE∥BF,
∴$\frac{AE}{BF}$=$\frac{AC}{BC}$=$\frac{3}{1}$,
∴$\frac{3}{BF}$=$\frac{3}{1}$,
∴BF=1,
∴B(-6,-1).
②当点B在第一象限时,作AE⊥x轴于E,BF⊥x轴于F,
∵AE∥BF,
∴$\frac{AE}{BF}$=$\frac{AC}{BC}$=$\frac{3}{1}$,
∴$\frac{3}{BF}$=$\frac{3}{1}$,
∴BF=1,
∴B(6,1),
综上所述,满足条件的点B坐标为(-6,-1)或(6,1).
点评 本题考查一次函数与反比例函数图象的交点,平行线分线段成比例定理等知识,解题的关键是学会添加常用辅助线,学会用分类退了的思想思考问题,属于中考常考题型.

练习册系列答案
相关题目
8.计算x-y-(x+y)的结果是( )
| A. | 2x-2y | B. | -2y | C. | -2x | D. | 0 |
15.多项式$\frac{1}{2}$x|m|-(m-2)x+7是关于x的二次三项式,则m的值为( )
| A. | 2 | B. | -2 | C. | ±2 | D. | 3 |
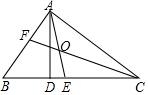 如图,在△ABC中,∠BAC=90°,∠B=50°,AE,CF是角平分线,它们相交于为O,AD是高,求∠BAD和∠AOC的度数.
如图,在△ABC中,∠BAC=90°,∠B=50°,AE,CF是角平分线,它们相交于为O,AD是高,求∠BAD和∠AOC的度数.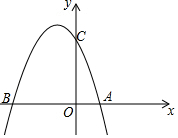 已知抛物线y=ax2+bx+3(a≠0)交x轴于A(1,0)和B (-3,0),交y轴于C.
已知抛物线y=ax2+bx+3(a≠0)交x轴于A(1,0)和B (-3,0),交y轴于C.