题目内容
18.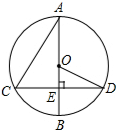 如图,在⊙O中,直径AB⊥CD,垂足为E,∠BOD=48°,则∠BAC的大小是( )
如图,在⊙O中,直径AB⊥CD,垂足为E,∠BOD=48°,则∠BAC的大小是( )| A. | 60° | B. | 48° | C. | 30° | D. | 24° |
分析 先根据垂径定理得到$\widehat{BC}$=$\widehat{BD}$,然后根据圆周角定理求解.
解答 解:∵直径AB⊥CD,
∴$\widehat{BC}$=$\widehat{BD}$,
∴∠BAC=$\frac{1}{2}$∠BOD=$\frac{1}{2}$×48°=24°.
故选D.
点评 本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.也考查了垂径定理.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
3.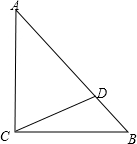 如图,在△ABC中,∠ACB=90°,AC=BC=AD.
如图,在△ABC中,∠ACB=90°,AC=BC=AD.
(1)作∠A的平分线交CD于E;
(2)过B作CD的垂线,垂足为F;
(3)请写出图中两对全等三角形(不添加任何字母),并选择其中一对加以证明.
 如图,在△ABC中,∠ACB=90°,AC=BC=AD.
如图,在△ABC中,∠ACB=90°,AC=BC=AD.(1)作∠A的平分线交CD于E;
(2)过B作CD的垂线,垂足为F;
(3)请写出图中两对全等三角形(不添加任何字母),并选择其中一对加以证明.
10.下面的计算正确的是( )
| A. | 6a-5a=1 | B. | $\sqrt{36}$=±6 | C. | (a2)3=a5 | D. | 2(a+b)=2a+2b |
7.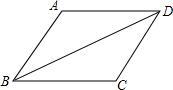 如图,在菱形ABCD中,AB=6,∠ABD=30°,则菱形ABCD的面积是( )
如图,在菱形ABCD中,AB=6,∠ABD=30°,则菱形ABCD的面积是( )
 如图,在菱形ABCD中,AB=6,∠ABD=30°,则菱形ABCD的面积是( )
如图,在菱形ABCD中,AB=6,∠ABD=30°,则菱形ABCD的面积是( )| A. | 18 | B. | 18$\sqrt{3}$ | C. | 36 | D. | 36$\sqrt{3}$ |
 已知函数y=$\frac{6}{x}$-1与函数y=kx交于点A(2,b)、B(-3,m)两点(点A在第一象限),
已知函数y=$\frac{6}{x}$-1与函数y=kx交于点A(2,b)、B(-3,m)两点(点A在第一象限),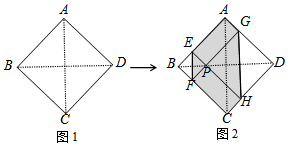 如图1,正方形纸片ABCD的边长为2,翻折∠B、∠D,使两个直角的顶点重合于对角线BD上一点P、EF、GH分别是折痕(如图2).设AE=x(0<x<2),给出下列判断:
如图1,正方形纸片ABCD的边长为2,翻折∠B、∠D,使两个直角的顶点重合于对角线BD上一点P、EF、GH分别是折痕(如图2).设AE=x(0<x<2),给出下列判断: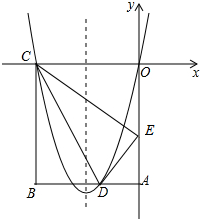 如图,在矩形OABC中,OA=5,AB=4,点D为边AB上一点,将△BCD沿直线CD折叠,使点B恰好落在边OA上的点E处,分别以OC,OA所在的直线为x轴,y轴建立平面直角坐标系.
如图,在矩形OABC中,OA=5,AB=4,点D为边AB上一点,将△BCD沿直线CD折叠,使点B恰好落在边OA上的点E处,分别以OC,OA所在的直线为x轴,y轴建立平面直角坐标系.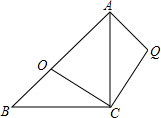 如图,等腰直角△ABC中,AC=BC,∠ACB=90°,点O分斜边AB为BO:OA=1:$\sqrt{3}$,将△BOC绕C点顺时针方向旋转到△AQC的位置,则∠AQC=105°.
如图,等腰直角△ABC中,AC=BC,∠ACB=90°,点O分斜边AB为BO:OA=1:$\sqrt{3}$,将△BOC绕C点顺时针方向旋转到△AQC的位置,则∠AQC=105°.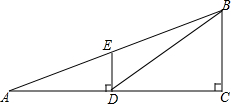 如图,观测点A、旗杆DE的底端D、某楼房CB的底端C三点在一条直线上,从点A处测得楼顶端B的仰角为22°,此时点E恰好在AB上,从点D处测得楼顶端B的仰角为38.5°.已知旗杆DE的高度为12米,试求楼房CB的高度.(参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40,sin38.5°≈0.62,cos38.5°≈0.78,tan38.5°≈0.80)
如图,观测点A、旗杆DE的底端D、某楼房CB的底端C三点在一条直线上,从点A处测得楼顶端B的仰角为22°,此时点E恰好在AB上,从点D处测得楼顶端B的仰角为38.5°.已知旗杆DE的高度为12米,试求楼房CB的高度.(参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40,sin38.5°≈0.62,cos38.5°≈0.78,tan38.5°≈0.80)