题目内容
3.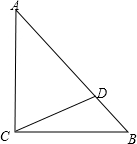 如图,在△ABC中,∠ACB=90°,AC=BC=AD.
如图,在△ABC中,∠ACB=90°,AC=BC=AD.(1)作∠A的平分线交CD于E;
(2)过B作CD的垂线,垂足为F;
(3)请写出图中两对全等三角形(不添加任何字母),并选择其中一对加以证明.
分析 (1)利用角平分线的作法得出∠A的平分线即可;
(2)利用钝角三角形高线的作法得出BF即可;
(3)利用等腰三角形的性质结合全等三角形的判定方法得出答案.
解答 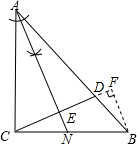 解:(1)如图所示:AE即为所求;
解:(1)如图所示:AE即为所求;
(2)如图所示:BF即为所求;
(3)如图所示:△ACE≌△ADE,△ACE≌△CFB,
证明:∵AC=AD,AE平分∠CAD,
∴AE⊥CD,EC=DE,
在△ACE和△ADE中
∵$\left\{\begin{array}{l}{AE=AE}\\{∠AEC=∠AED}\\{EC=ED}\end{array}\right.$,
∴△ACE≌△ADE(SAS).
点评 此题主要考查了复杂作图以及全等三角形的判定,熟练掌握全等三角形的判定方法是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.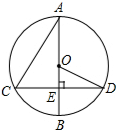 如图,在⊙O中,直径AB⊥CD,垂足为E,∠BOD=48°,则∠BAC的大小是( )
如图,在⊙O中,直径AB⊥CD,垂足为E,∠BOD=48°,则∠BAC的大小是( )
 如图,在⊙O中,直径AB⊥CD,垂足为E,∠BOD=48°,则∠BAC的大小是( )
如图,在⊙O中,直径AB⊥CD,垂足为E,∠BOD=48°,则∠BAC的大小是( )| A. | 60° | B. | 48° | C. | 30° | D. | 24° |
15.△ABC是一个任意三角形,用直尺和圆规作出∠A、∠B的平分线,如果两条平分线交于点O,那么下列选项中不正确的是( )
| A. | 点O一定在△ABC的内部 | B. | ∠C的平分线一定经过点O | ||
| C. | 点O到△ABC的三边距离一定相等 | D. | 点O到△ABC三顶点的距离一定相等 |
13.下列图形中,是轴对称图形,但不是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
 如图,在平行四边形ABCD中,点E为边AD的中点,连接AC,BE交于点O,则S△AOE:S△COB=1:4.
如图,在平行四边形ABCD中,点E为边AD的中点,连接AC,BE交于点O,则S△AOE:S△COB=1:4.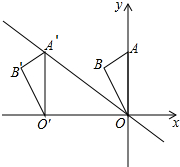 如图,在平面直角坐标系中,点A的坐标为(0,6),将△OAB沿x轴向左平移得到△O′A′B′,点A的对应点A′落在直线y=-$\frac{3}{4}$x上,则点B与其对应点B′间的距离为8.
如图,在平面直角坐标系中,点A的坐标为(0,6),将△OAB沿x轴向左平移得到△O′A′B′,点A的对应点A′落在直线y=-$\frac{3}{4}$x上,则点B与其对应点B′间的距离为8. .
.