题目内容
8. 已知函数y=$\frac{6}{x}$-1与函数y=kx交于点A(2,b)、B(-3,m)两点(点A在第一象限),
已知函数y=$\frac{6}{x}$-1与函数y=kx交于点A(2,b)、B(-3,m)两点(点A在第一象限),(1)求b,m,k的值;
(2)函数与x轴交于点C,求△ABC的面积.
分析 (1)把点A(2,b),B(-3,m)代入函数的解析式即可得到结果;
(2)先求出函数y=$\frac{6}{x}$-1与x轴交点C,即可求得结果.
解答 解:(1)∵点A(2,b),B(-3,m)在y=$\frac{6}{x}$-1上,
∴$\left\{\begin{array}{l}{b=\frac{6}{2}-1}\\{m=\frac{6}{-3}-1}\end{array}\right.$,解得b=2,m=-3,
∴把A(2,2)代入y=kx,
∴k=1;
(2)∵函数y=$\frac{6}{x}$-1与x轴交于点C,
∴C(6,0),
∴S△ABC=S△AOC+S△BOC=$\frac{1}{2}$×6×2$+\frac{1}{2}×6×3$=15.
点评 本题考查了一次函数和反比例函数的交点问题,三角形的面积的求法,求点的坐标,正确的识别图形是解题的关键.

练习册系列答案
相关题目
19.若三角形的三边长分别为3,4,x,则x的值可能是( )
| A. | 1 | B. | 6 | C. | 7 | D. | 10 |
18.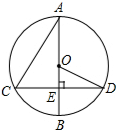 如图,在⊙O中,直径AB⊥CD,垂足为E,∠BOD=48°,则∠BAC的大小是( )
如图,在⊙O中,直径AB⊥CD,垂足为E,∠BOD=48°,则∠BAC的大小是( )
 如图,在⊙O中,直径AB⊥CD,垂足为E,∠BOD=48°,则∠BAC的大小是( )
如图,在⊙O中,直径AB⊥CD,垂足为E,∠BOD=48°,则∠BAC的大小是( )| A. | 60° | B. | 48° | C. | 30° | D. | 24° |
 已知一次函数y=kx+b的图象与直线y=-$\sqrt{3}$x平行且经过点(2,-$\sqrt{3}$),与x轴、y轴分别交于A,B两点.
已知一次函数y=kx+b的图象与直线y=-$\sqrt{3}$x平行且经过点(2,-$\sqrt{3}$),与x轴、y轴分别交于A,B两点.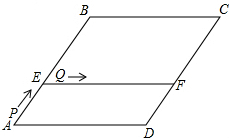 如图,在菱形ABCD中,AB=10,sinA=$\frac{4}{5}$,点E在AB上,AE=4,过点E作EF∥AD,交CD于点F.
如图,在菱形ABCD中,AB=10,sinA=$\frac{4}{5}$,点E在AB上,AE=4,过点E作EF∥AD,交CD于点F.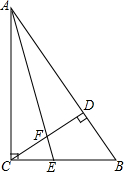 已知,如图,在△ABC中,∠ACB=90°,AE是角平分线,CD是高,AE、CD相交于点F,求证:∠CEF=∠CFE.
已知,如图,在△ABC中,∠ACB=90°,AE是角平分线,CD是高,AE、CD相交于点F,求证:∠CEF=∠CFE. 已知,如图,△OBC中是直角三角形,OB与x轴正半轴重合,∠OBC=90°,且OB=1,BC=$\sqrt{3}$,将△OBC绕原点O逆时针旋转60°再将其各边扩大为原来的2倍,使OB1=OC,得到△OB1C1,将△OB1C1绕原点O逆时针旋转60°再将其各边扩大为原来的2倍,使OB2=OC1,得到△OB2C2,…,如此继续下去,得到△OB2015C2015,则点C2015的坐标是(22016,0).
已知,如图,△OBC中是直角三角形,OB与x轴正半轴重合,∠OBC=90°,且OB=1,BC=$\sqrt{3}$,将△OBC绕原点O逆时针旋转60°再将其各边扩大为原来的2倍,使OB1=OC,得到△OB1C1,将△OB1C1绕原点O逆时针旋转60°再将其各边扩大为原来的2倍,使OB2=OC1,得到△OB2C2,…,如此继续下去,得到△OB2015C2015,则点C2015的坐标是(22016,0).