Question

11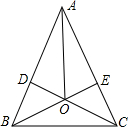．如图，在△ABC中，CD⊥AB于点D，BE⊥AC于点E，CD=BE，BE与CD相交于点O．连结OA，试判断直线OA、BC的位置关系，并说明理由．

Answer 1

分析 利用AAS证明△ADC≌△AEB，根据全等得出AE=AD，∠ABO=∠ACO，求出BD=CE，证△DBO≌△ECO，推出BO=CO，即可得出答案．

解答 解：OA⊥BC，
理由是：∵CD⊥AB于点D，BE⊥AC于点E，
∴∠AEB=∠ADC=90°，
在△ADC和△AEB中，
$\left\{\begin{array}{l}{∠ADC=∠AEB}\\{∠CAD=∠BAE}\\{CD=BE}\end{array}\right.$，
∴△ADC≌△AEB（AAS），
∴AE=AD，∠ABO=∠ACO，
∵AB=AC，
∴AB-AD=AC-AE，
即DB=EC，
在△DBO和△ECO中，
$\left\{\begin{array}{l}{∠DOB=∠EOC}\\{∠DBO=∠ECO}\\{BD=CE}\end{array}\right.$，
∴△DBO≌△ECO（AAS），
∴BO=CO，
∴点O在BC的垂直平分线上，
∵AB=AC，
∴点A在BC的垂直平分线上，
∴AO垂直平分BC．

点评 此题主要考查了全等三角形的判定与性质，线段垂直平分线性质的应用，解此题的关键是推出AB=AC和OB=OC．