题目内容
3. 已知:Rt△ABC≌Rt△ADE,∠ABC=∠ADE=90°,BC与DE相交于点F,连结CD、EB.
已知:Rt△ABC≌Rt△ADE,∠ABC=∠ADE=90°,BC与DE相交于点F,连结CD、EB.(1)请找出图中其他的全等三角形;
(2)求证:CD=EB;
(3)求证:CF=EF.
分析 (1)根据题意和图形作答即可;
(2)根据三角形全等的判定定理证明△ADC≌△ABE,根据全等三角形的性质证明;
(3)根据三角形全等的判定定理证明△DFC≌△BFE,根据全等三角形的性质证明即可.
解答 解:(1)△ADC≌△ABE;△CDF≌△EBF;
(2)证明:∵Rt△ABC≌Rt△ADE,
∴AC=AE,AD=AB.∠BAC=∠DAE,∠BAC-∠DAB=∠DAE-∠DAB,
∴∠DAC=∠BAE.
∴△ADC≌△ABE,
∴CD=BE;
(3)证明:由(2)得 CD=BE,∠ACD=∠AEB.
∵Rt△ABC≌Rt△ADE,
∴∠ACB=∠AED.∠ACB-∠ACD=∠AED-∠AEB,
∴∠DCF=∠BEF.∠DFC=∠BFE,
∴△DFC≌△BFE(AAS),
∴CF=EF.
点评 本题考查的是全等三角形的判定和性质,掌握三角形全等的判定定理:SSS、SAS、AAS或ASA以及直角三角形的HL以及全等三角形的对应边相等、对应角相等是解题的关键.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
13. 二次函数y=-x2-6x-2的图象如图所示,若点A(1,y1),B(2,y2)是图象上的两点,则y1与y2的大小关系是( )
二次函数y=-x2-6x-2的图象如图所示,若点A(1,y1),B(2,y2)是图象上的两点,则y1与y2的大小关系是( )
 二次函数y=-x2-6x-2的图象如图所示,若点A(1,y1),B(2,y2)是图象上的两点,则y1与y2的大小关系是( )
二次函数y=-x2-6x-2的图象如图所示,若点A(1,y1),B(2,y2)是图象上的两点,则y1与y2的大小关系是( )| A. | y1<y2 | B. | y1=y2 | C. | y1>y2 | D. | 不能确定 |
7.若-3xmy4与7x2yn-1是同类项,则m+n的值为( )
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
8.已知x,y为实数,且$\sqrt{x-1}$+3|y-2|=0,则x-y的值为( )
| A. | 3 | B. | -3 | C. | -1 | D. | 1 |
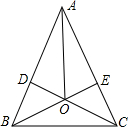 如图,在△ABC中,CD⊥AB于点D,BE⊥AC于点E,CD=BE,BE与CD相交于点O.连结OA,试判断直线OA、BC的位置关系,并说明理由.
如图,在△ABC中,CD⊥AB于点D,BE⊥AC于点E,CD=BE,BE与CD相交于点O.连结OA,试判断直线OA、BC的位置关系,并说明理由. 如图,直线AB、CD相交于O,OE平分∠AOC,若∠AOE=23°,则∠BOD=46°.
如图,直线AB、CD相交于O,OE平分∠AOC,若∠AOE=23°,则∠BOD=46°. 将一副直角三角尺如图叠放,若∠AOD=15°,则∠BOC=165°.
将一副直角三角尺如图叠放,若∠AOD=15°,则∠BOC=165°.