题目内容
如果等腰三角形的一边长为6cm,周长为14cm,那么另外两边的长分别为 .
考点:等腰三角形的性质,三角形三边关系
专题:
分析:分6cm是腰长和底边两种情况求出三角形的另外两边,再利用三角形的三边关系判断即可得解.
解答:解:①若6cm是腰长,则另两边分别为6cm,2cm,
能组成三角形,
②若6cm是底边,则另两边分别为4cm,4cm,
能组成三角形,
所以,那么另外两边的长分别为6cm,2cm或4cm,4cm.
故答案为:6cm,2cm或4cm,4cm.
能组成三角形,
②若6cm是底边,则另两边分别为4cm,4cm,
能组成三角形,
所以,那么另外两边的长分别为6cm,2cm或4cm,4cm.
故答案为:6cm,2cm或4cm,4cm.
点评:本题考查了等腰三角形的性质,主要利用了等腰三角形两腰相等的性质,难点在于分情况讨论并注意从三角形的三边关系判断是否能组成三角形.

练习册系列答案
相关题目
对于函数y=3(x-2)2,下列说法正确的是( )
| A、当x>0时,y随x的增大而减小 |
| B、当x<0时,y随x的增大而增大 |
| C、当x>2时,y随x的增大而增大 |
| D、当x>-2时,y随x的增大而减小 |
 在如图所示的平面直角坐标系中,桥孔抛物线对应的二次函数关系式是y=-
在如图所示的平面直角坐标系中,桥孔抛物线对应的二次函数关系式是y=-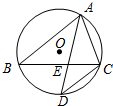 如图,⊙O是△ABC的外接圆,∠BAC的角平分线交BC于点E,交⊙O于点D,若AE=AC.求证:AB=AD.
如图,⊙O是△ABC的外接圆,∠BAC的角平分线交BC于点E,交⊙O于点D,若AE=AC.求证:AB=AD. 如图,在直角坐标系中,△AOB是等边三角形,若B点的坐标是(2,0),则A点的坐标是
如图,在直角坐标系中,△AOB是等边三角形,若B点的坐标是(2,0),则A点的坐标是