题目内容
2.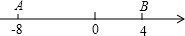 如图,数轴上两个动点A、B起始位置所表示的数分别为-8,4,A、B两点各自以一定的速度在数轴上运动,已知A点的运动速度为2个单位/秒.
如图,数轴上两个动点A、B起始位置所表示的数分别为-8,4,A、B两点各自以一定的速度在数轴上运动,已知A点的运动速度为2个单位/秒.(1)若A、B两点同时出发相向而行,正好在原点处相遇,请直接写出B点的运动速度;
(2)若A、B两点于起始位置按上述速度同时出发,向数轴正方向运动,几秒钟时两点相距6个单位长度?
(3)若A、B两点于起始位置按上述速度同时出发,向数轴负方向运动,与此同时,C点从原点出发作同方向的运动,如果在运动过程中,始终有CA=2CB,求C点的运动速度.
分析 (1)根据速度=路程÷时间,即可解决问题;
(2)由OA+OB大于6个单位长度,分两种情况,一种B在右侧,一种A点在右侧,再根据时间=路程÷时间,即可解决问题;
(3)要想始终保持CA=2CB,则C点的速度应介于A、B两者之间,设出C点速度为x个单位/秒,联立方程,解方程即可得出结论.
解答 解:(1)B点的运动速度为OB÷$\frac{OA}{2}$=4÷$\frac{8}{2}$=1个单位/秒.
(2)∵OA+OB=8+4=12>6,且A点运动速度大于B点的速度,
∴分两种情况,
①当点B在点A的右侧时,
运动时间为$\frac{OA+OB-6}{2-1}$=$\frac{12-6}{1}$=6s.
②当点A在点B的右侧时,
运动时间为$\frac{OA+OB+6}{2-1}$=$\frac{12+6}{1}$=18s.
综合①②得,6秒和18秒时,两点相距都是6个单位长度.
(3)设点C的运动速度为x个单位/秒,运动时间为t,根据题意得知
8+(2-x)×t=[4+(x-1)×t]×2,
整理,得2-x=2x-2,
解得x=$\frac{4}{3}$.
故C点的运动速度为$\frac{4}{3}$个单位/秒.
点评 本题考查了两点间的距离和一元一次方程的应用,解题的关键:(1)牢记速度=路程÷时间;(2)分两种情况,再结合时间=路程÷速度即可;(3)设出C点速度,联立方程,求解一元一次方程,能熟练的运用解一元一次方程来解决实际问题.

练习册系列答案
相关题目
12.位于江汉平原的兴隆水利枢纽工程于2014年9月25日竣工,该工程设计的年发电量为2.25亿度,那么这个数值( )
| A. | 精确到亿位 | B. | 精确到百分位 | C. | 精确到千万位 | D. | 精确到百万位 |
 如图,以G(0,1)为圆心,半径为2的圆与x轴交于A、B两点,与y轴交于C、D两点,点E为⊙G上一动点,CF⊥AE于F,当点E从B点出发顺时针运动到D点时,点F经过的路径长为$\frac{\sqrt{3}}{3}$π.
如图,以G(0,1)为圆心,半径为2的圆与x轴交于A、B两点,与y轴交于C、D两点,点E为⊙G上一动点,CF⊥AE于F,当点E从B点出发顺时针运动到D点时,点F经过的路径长为$\frac{\sqrt{3}}{3}$π. 如图,已知△ABC是等边三角形,D是BC的中点,BH∥AC.
如图,已知△ABC是等边三角形,D是BC的中点,BH∥AC. 综合与探究:
综合与探究: