题目内容
12.解方程:(1)4(x-1)-1=3(x-2)
(2)$\frac{2x+1}{3}$-$\frac{5x-1}{6}$=1.
分析 (1)方程去括号,移项合并,把x系数化为1,即可求出解;
(2)方程去分母,去括号,移项合并,把x系数化为1,即可求出解.
解答 解:(1)去括号得:4x-4-1=3x-6,
移项合并得:x=-1;
(2)去分母得:4x+2-5x+1=6,
移项合并得:-x=3,
解得:x=-3.
点评 此题考查了解一元一次方程,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
20. 如图,已知线段AB两个端点的坐标分别为A(6,6),B(8,4),以原点O为位似中心,在第一象限内将线段AB缩小为原来的$\frac{1}{2}$后得到线段CD,则端点D的坐标为( )
如图,已知线段AB两个端点的坐标分别为A(6,6),B(8,4),以原点O为位似中心,在第一象限内将线段AB缩小为原来的$\frac{1}{2}$后得到线段CD,则端点D的坐标为( )
 如图,已知线段AB两个端点的坐标分别为A(6,6),B(8,4),以原点O为位似中心,在第一象限内将线段AB缩小为原来的$\frac{1}{2}$后得到线段CD,则端点D的坐标为( )
如图,已知线段AB两个端点的坐标分别为A(6,6),B(8,4),以原点O为位似中心,在第一象限内将线段AB缩小为原来的$\frac{1}{2}$后得到线段CD,则端点D的坐标为( )| A. | (4,2) | B. | (2,4) | C. | (3,3) | D. | (4,2)或(-4,2) |
7.下列几何体中,从正面看形状图相同的是( )

| A. | ①② | B. | ①③ | C. | ①④ | D. | ②④ |
17.从3,4,5三个数中随机抽取两个数,则取出的两个数都是奇数的概率为( )
| A. | 0 | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | 1 |
4.(-1)4可表示为( )
| A. | (-1)×4 | B. | (-1)+(-1)+(-1)+(-1) | C. | -1×1×1×1 | D. | (-1)×(-1)×(-1)×(-1) |
1. 如图在平面直角坐标系中,点A,B,C的坐标分别为A(2,3),B(5,0),C(4,1),则△AOC的面积是( )
如图在平面直角坐标系中,点A,B,C的坐标分别为A(2,3),B(5,0),C(4,1),则△AOC的面积是( )
 如图在平面直角坐标系中,点A,B,C的坐标分别为A(2,3),B(5,0),C(4,1),则△AOC的面积是( )
如图在平面直角坐标系中,点A,B,C的坐标分别为A(2,3),B(5,0),C(4,1),则△AOC的面积是( )| A. | 5 | B. | 10 | C. | 75 | D. | 15 |
2.已知反比例函数y=$\frac{a}{x}$(a≠0)的图象,在第一象限内,y的值随x值的增大而减小,则一次函数y=ax+a的图象不经过( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
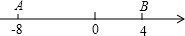 如图,数轴上两个动点A、B起始位置所表示的数分别为-8,4,A、B两点各自以一定的速度在数轴上运动,已知A点的运动速度为2个单位/秒.
如图,数轴上两个动点A、B起始位置所表示的数分别为-8,4,A、B两点各自以一定的速度在数轴上运动,已知A点的运动速度为2个单位/秒.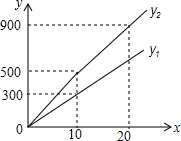 为发展旅游经济,我市某景区对门票采用灵活的售票方法吸引游客.门票定价为50元/人,非节假日打a折售票,节假日按团队人数分段定价售票,即m人以下(含m人)的团队按原价售票;超过m人的团队,其中m人仍按原价售票,超过m人部分的游客打b折售票.设某旅游团人数为x人,非节假日购票款为y1(元),节假日购票款为y2(元).y1与y2之间的函数图象如图所示.
为发展旅游经济,我市某景区对门票采用灵活的售票方法吸引游客.门票定价为50元/人,非节假日打a折售票,节假日按团队人数分段定价售票,即m人以下(含m人)的团队按原价售票;超过m人的团队,其中m人仍按原价售票,超过m人部分的游客打b折售票.设某旅游团人数为x人,非节假日购票款为y1(元),节假日购票款为y2(元).y1与y2之间的函数图象如图所示.