题目内容
8．计算：（$\frac{1}{x}$+$\frac{1}{y}$+$\frac{1}{z}$）÷$\frac{xy+yz+xz}{xy}$=$\frac{1}{z}$．分析 先通分，再将除法化为乘法，约分即可．
解答 解：（$\frac{1}{x}$+$\frac{1}{y}$+$\frac{1}{z}$）÷$\frac{xy+yz+xz}{xy}$，
=$\frac{yz+zx+xy}{xyz}$•$\frac{xy}{xy+yz+xz}$，
=$\frac{1}{z}$，
故答案为：$\frac{1}{z}$．
点评 本题是分式的混合运算，解答本题的关键在于熟练掌握分式混合运算的运算法则．
练习册系列答案
王后雄学案教材完全解读系列答案
海淀课时新作业金榜卷系列答案
相关题目
如图，在△ABC中，若sinA=$\frac{1}{3}$，则tanA的值是$\frac{\sqrt{2}}{4}$．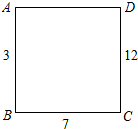
如图，在正方形ABCD的每个顶点上写一个数，把这个正方形每条边的两端点上的