题目内容
18. 如图,直线AB、BC、CD分别与⊙O相切于A、E、D,且AB∥CD,若OB=6cm,OC=8cm,求
如图,直线AB、BC、CD分别与⊙O相切于A、E、D,且AB∥CD,若OB=6cm,OC=8cm,求(1)∠BOC 的度数;
(2)⊙O的半径;
(3)AB+CD的值.
分析 (1)连接OA,OE,证明Rt△OAB≌Rt△OEB,由此可得∠ABO=∠OBE,再由平行的性质即可求解∠BOC 的度数;
(2)由勾股定理求得BC,再由三角形的面积求得⊙O的半径.
(3)利用(1)中所得AB=BE、CE=CD即可.
解答 解:(1)连接OA,OE.
∵直线AB、BC、CD分别与⊙O相切于A、E、D,
∴OA⊥AB,OE⊥BC,
∴∠OAB=∠OEB=90°,OA=OE
在Rt△OAB 与Rt△OEB中
$\left\{\begin{array}{l}{OA=OE}\\{OB=OB}\end{array}\right.$
∴Rt△OAB≌Rt△OEB(HL)
∴∠ABO=∠OBE,AB=BE
同理可证:∠OCE=∠OCD,CE=CD,
又∵AB∥CD,
∴∠ABC+∠DCB=180°,
∴∠OBC+∠OCB=90°,
∴∠BOC=90°
(2)在Rt△BOC中,BC=$\sqrt{O{B}^{2}+O{C}^{2}}$=10
∴$\frac{1}{2}$OB•OC=$\frac{1}{2}$BC•r
r=$\frac{6×8}{10}$=4.8
即:⊙O的半径为4.8
(3)由(1)可知:
AB=BE,CE=CD,
∴AB+CD=BE+CE=BC=10
即:BC的值为10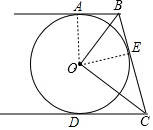
点评 本题考查了切线的性质,解题的关键是证明Rt△OAB≌Rt△OEB由此得出∠ABO=∠OBE

练习册系列答案
相关题目
6.平行四边形是一个不稳定的几何图形,现有一个平行四边形的对角线长是8cm和12cm,那么下列数据中符合一个平行四边形要求的边长( )
| A. | 2cm | B. | 9cm | C. | 10cm | D. | 20cm |
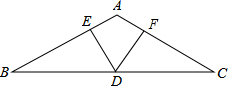 如图,在△ABC中,AB=AC,∠BAC=120°,D是BC边上的中点,过D点分别作AB,AC的垂线,垂足分别为E,F.
如图,在△ABC中,AB=AC,∠BAC=120°,D是BC边上的中点,过D点分别作AB,AC的垂线,垂足分别为E,F. 如图,在矩形ABCD中,点E、F分别在边AD、DC上,△ABE∽△DEF,AB=6,AE=9,DE=2,求EF的长.
如图,在矩形ABCD中,点E、F分别在边AD、DC上,△ABE∽△DEF,AB=6,AE=9,DE=2,求EF的长. 如图是由两个边长分别为a,b的正方形拼成的图形,用含字母的式子表示图中阴影部分的面积.
如图是由两个边长分别为a,b的正方形拼成的图形,用含字母的式子表示图中阴影部分的面积.