题目内容
5.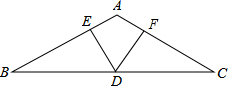 如图,在△ABC中,AB=AC,∠BAC=120°,D是BC边上的中点,过D点分别作AB,AC的垂线,垂足分别为E,F.
如图,在△ABC中,AB=AC,∠BAC=120°,D是BC边上的中点,过D点分别作AB,AC的垂线,垂足分别为E,F.(1)求证:DE+DF=$\frac{1}{2}$BC;
(2)当点D为BC上任意一点,其余条件不变时,(1)中的结论是否成立?请说明理由.
分析 (1)先根据等腰三角形的性质及三角形内角和定理求出∠B=∠C=30°,根据直角三角形30°角所对的直角边等于斜边的一半得到DE=$\frac{1}{2}$BD,DF=$\frac{1}{2}$DC,两式相加即可得出DE+DF=$\frac{1}{2}$BC.
(2)先作辅助线,构造含30°角的直角三角形,求得CG=$\frac{1}{2}$BC,再根据面积法,求得DE+DF=CG,最后得出结论.
解答  (1)证明:∵AB=AC,∠BAC=120°,
(1)证明:∵AB=AC,∠BAC=120°,
∴∠B=∠C=30°,
∵DE⊥AB,DF⊥AC,垂足为E,F,
∴DE=$\frac{1}{2}$BD,DF=$\frac{1}{2}$DC,
∴DE+DF=$\frac{1}{2}$BD+$\frac{1}{2}$DC=$\frac{1}{2}$(BD+DC)=$\frac{1}{2}$BC.
∴DE+DF=$\frac{1}{2}$BC.
(2)DE+DF=$\frac{1}{2}$BC成立.
理由:过点C作CG⊥AB,交AB的延长线于G,连接AD,
∵AB=AC,∠BAC=120°,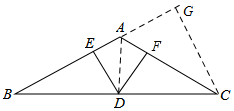
∴∠B=30°,
∴Rt△BCG中,CG=$\frac{1}{2}$BC,
又∵DE⊥AB,DF⊥AC,
∴$\frac{1}{2}$×AB×DE+$\frac{1}{2}$×AC×DF=$\frac{1}{2}$×AB×CG,
∴DE+DF=CG,
∴DE+DF=$\frac{1}{2}$BC.
点评 此题主要考查等腰三角形的性质,三角形内角和定理及含30度角的直角三角形的性质的综合运用,解题时注意:直角三角形中,30°角所对的直角边等于斜边的一半.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
 已知:如图,在Rt△ABC中,∠C=90°,∠B=30°,AD平分∠BAC.求证:点D在AB的垂直平分线上.
已知:如图,在Rt△ABC中,∠C=90°,∠B=30°,AD平分∠BAC.求证:点D在AB的垂直平分线上.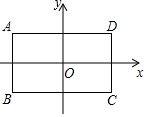 如图,分别以长方形ABCD的两条对称轴为x轴和y轴建立平面直角坐标系,若A点的坐标为(-4,3).
如图,分别以长方形ABCD的两条对称轴为x轴和y轴建立平面直角坐标系,若A点的坐标为(-4,3).
 如图,直线AB、BC、CD分别与⊙O相切于A、E、D,且AB∥CD,若OB=6cm,OC=8cm,求
如图,直线AB、BC、CD分别与⊙O相切于A、E、D,且AB∥CD,若OB=6cm,OC=8cm,求