题目内容
10．
如图，在矩形ABCD中，点E、F分别在边AD、DC上，△ABE∽△DEF，AB=6，AE=9，DE=2，求EF的长．
分析 先根据相似三角形的性质求出DF的长，再由勾股定理即可得出结论．
解答 解：∵△ABE∽△DEF，AB=6，AE=9，DE=2，
∴$\frac{AB}{DE}$=$\frac{AE}{DF}$，即$\frac{6}{2}$=$\frac{9}{DF}$，解得DF=3，
∴EF=$\sqrt{D{E}^{2}+D{F}^{2}}$=$\sqrt{{2}^{2}+{3}^{2}}$=$\sqrt{13}$．
点评 本题考查的是相似三角形的性质，熟知相似三角形的对应边成比例是解答此题的关键．
练习册系列答案
相关题目
如图，直线AB、BC、CD分别与⊙O相切于A、E、D，且AB∥CD，若OB=6cm，OC=8cm，求
如图，点P是?ABCD内的任意一点，连接PA、PB、PC、PD，得到△PAB、△PBC、△PCD、△PDA，设它们的面积分别是S1、S2、S3、S4，给出如下结论：
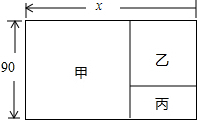列方程解应用题：如图，有一块长方形土地，长xm，宽90m（x大于90），建筑商把它分成甲、乙、丙三部分，其中甲和乙都是正方形，现在计划甲处修建广场，乙处修建商场，丙处修建住宅．已知丙的面积为1800m2，试求出原长方形土地的面积．
某市拟建造农民文化公园，将12个场馆排成6行，每行4个场馆，市政府将如图所示的设计图公布后，引起了一群初中生的浓厚兴趣，他们纷纷设计出许多精美的轴对称图形来，请你也设计一幅符合条件的图形．