题目内容
7.已知$\sqrt{a-12}$+$\sqrt{15-b}$=0,求$\frac{1}{\sqrt{a}}$+$\frac{\sqrt{5}}{\sqrt{b}}$的值.分析 根据非负数的性质列出算式,求出a、b的值,根据二次根式的混合运算法则计算即可.
解答 解:由已知得,a-12=0,15-b=0,
解得,a=12,b=15,
原式=$\frac{1}{\sqrt{12}}$+$\frac{\sqrt{5}}{\sqrt{15}}$=$\frac{1}{2\sqrt{3}}$+$\frac{1}{\sqrt{3}}$=$\frac{\sqrt{3}}{2}$.
点评 本题考查的是非负数的性质,掌握当几个非负数相加和为0时,则其中的每一项都必须等于0是解题的关键.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目
 如图,直线AB、BC、CD分别与⊙O相切于A、E、D,且AB∥CD,若OB=6cm,OC=8cm,求
如图,直线AB、BC、CD分别与⊙O相切于A、E、D,且AB∥CD,若OB=6cm,OC=8cm,求



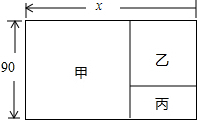 列方程解应用题:如图,有一块长方形土地,长xm,宽90m(x大于90),建筑商把它分成甲、乙、丙三部分,其中甲和乙都是正方形,现在计划甲处修建广场,乙处修建商场,丙处修建住宅.已知丙的面积为1800m2,试求出原长方形土地的面积.
列方程解应用题:如图,有一块长方形土地,长xm,宽90m(x大于90),建筑商把它分成甲、乙、丙三部分,其中甲和乙都是正方形,现在计划甲处修建广场,乙处修建商场,丙处修建住宅.已知丙的面积为1800m2,试求出原长方形土地的面积. 如图,等边△ABC的边长为2$\sqrt{3}$,以BC边所在直线为x轴,BC边上的高线AO所在的直线为y轴建立平面直角坐标系.
如图,等边△ABC的边长为2$\sqrt{3}$,以BC边所在直线为x轴,BC边上的高线AO所在的直线为y轴建立平面直角坐标系. 已知,如图,在△ABC中,AB=AC,以点A为圆心画弧分别交CA的延长线、AB于E,F,联结EF并延长交BC于G,求证:EG⊥BC.
已知,如图,在△ABC中,AB=AC,以点A为圆心画弧分别交CA的延长线、AB于E,F,联结EF并延长交BC于G,求证:EG⊥BC.