题目内容
11.小数在数学外小组活动中遇到这样一个问题:如果α、β都为锐角,且tanα=$\frac{1}{2}$,tanβ=$\frac{1}{3}$.求α+β的度数.(1)小敏是这样解决问题的:如图1,把α,β放在正方形网格中,使得∠ABD=α,∠CBE=β,且BA,BC在直线BD的两侧,连接AC,可证得△ABC是等腰直角三角形,因此可求得α+β=∠ABC=45°.
(2)请你参考小敏思考问题的方法解决问题:如果α,β都为锐角,当tanα=4,tanβ=$\frac{3}{5}$时,在图2的正方形网格中,利用已作出的锐角α,画出∠MON=α-β,由此可得α-β=45°.

分析 如图1,把α,β放在正方形网格中,使得∠ABD=α,∠CBE=β,且BA,BC在直线BD的两侧,连接AC,可证得△ABC是等腰三角形,可求得α+β=∠ABC=45°;
如图2,把α,β放在正方形网格中,使得∠MOG=α,∠NOH=β,且ON在∠MOG内,连接MN,可证得△MON是等腰三角形,可求得α-β=45°.
解答 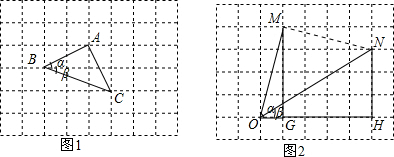 解:如图1,把α,β放在正方形网格中,使得∠ABD=α,∠CBE=β,且BA,BC在直线BD的两侧,连接AC,可证得△ABC是等腰三角形,
解:如图1,把α,β放在正方形网格中,使得∠ABD=α,∠CBE=β,且BA,BC在直线BD的两侧,连接AC,可证得△ABC是等腰三角形,
因此可求得α+β=∠ABC=45°;
参考小敏思考问题的方法解决问题:
如果α,β都为锐角,当tanα=4,tanβ=$\frac{3}{5}$时,在图2的正方形网格中,利用已作出的锐角α,画出∠MON=α-β,由此可得α-β=45°.
故答案为:45;45.
点评 本题考查了作图-应用与设计图,等腰三角形的性质,解直角三角形等,根据函数值作出直角三角形是解题的关键.

练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
16.点P,Q都是直线l外的点,下列说法正确的是( )
| A. | 连接PQ,则PQ一定与直线l垂直 | B. | 连接PQ,则PQ一定与直线l平行 | ||
| C. | 连接PQ,则PQ一定与直线l相交 | D. | 过点P只能画一条直线与直线l平行 |
3. 如图,能判断直线AB∥CD的条件是( )
如图,能判断直线AB∥CD的条件是( )
 如图,能判断直线AB∥CD的条件是( )
如图,能判断直线AB∥CD的条件是( )| A. | ∠1=∠2 | B. | ∠1+∠3=180° | C. | ∠3=∠4 | D. | ∠3+∠4=180° |
 如图,在矩形ABCD中,AB=8,BC=6,将矩形沿EF折叠,使顶点B与D重合,则折痕EF的长为7.5.
如图,在矩形ABCD中,AB=8,BC=6,将矩形沿EF折叠,使顶点B与D重合,则折痕EF的长为7.5. 如图,一个正方体的棱长为2cm,一只蚂蚁欲从A点处沿正方体侧面到B点处吃食物,那么它需要爬行的最短路径的长是2$\sqrt{5}$cm.
如图,一个正方体的棱长为2cm,一只蚂蚁欲从A点处沿正方体侧面到B点处吃食物,那么它需要爬行的最短路径的长是2$\sqrt{5}$cm. 如图,△ABC中,DA=DB,将△CBD沿CD翻折,使B点落在平面ACD内的一点E处.若△ACD与△ECD重叠部分的面积是△ABC的面积的$\frac{1}{4}$,AB=6,求AC的长.
如图,△ABC中,DA=DB,将△CBD沿CD翻折,使B点落在平面ACD内的一点E处.若△ACD与△ECD重叠部分的面积是△ABC的面积的$\frac{1}{4}$,AB=6,求AC的长.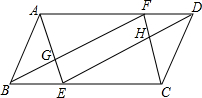 如图,在?ABCD中,AB=2,BC=4,∠ABC=60°,E,F分别是BC,AD上的两点,且BE=DF,连AE,BF,DE,CF分别交于点G,H.
如图,在?ABCD中,AB=2,BC=4,∠ABC=60°,E,F分别是BC,AD上的两点,且BE=DF,连AE,BF,DE,CF分别交于点G,H.