题目内容
6.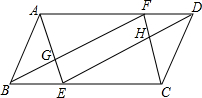 如图,在?ABCD中,AB=2,BC=4,∠ABC=60°,E,F分别是BC,AD上的两点,且BE=DF,连AE,BF,DE,CF分别交于点G,H.
如图,在?ABCD中,AB=2,BC=4,∠ABC=60°,E,F分别是BC,AD上的两点,且BE=DF,连AE,BF,DE,CF分别交于点G,H.(1)求证:四边形GEHF是平行四边形.
(2)若E,F分别是BC,AD上的两个动点,设BE=DF=x,试推断当x等于多少时,四边形GEHF是矩形.
分析 (1)由平行四边形的性质得出AD∥BC,AD=BC,证明四边形FBED是平行四边形,得出BF∥ED,同理:四边形AECF是平行四边形,得出AE∥FC,即可得出结论;
(2)由平行四边形的性质得出∠BAD=120°,证明△ABE是等边三角形,得出BE=DF=AB=2,证出AB=AF,得出∠ABG=∠AFG=30°,证出∠EGF=90°,即可得出四边形GEHF是矩形.
解答 (1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴BE∥DF,
∵BE=DF,
∴四边形FBED是平行四边形,
∴BF∥ED,即GF∥EH,
同理:四边形AECF是平行四边形,
∴AE∥FC,
即GE∥FH,
∴四边形GEHF是平行四边形;
(2)解:当AE平分∠BAD,CF平分∠BCD时,BE=DF=2,四边形GEHF是矩形;理由如下:
∵四边形ABCD是平行四边形,
∴∠BAD=180°-∠ABC=180°-60°=120°,
∴∠ABC=∠BAC=∠AEB=60°,
∴△ABE是等边三角形,
∴BE=DF=AB=2,
∴AF=CE=BC-BE=4-2=2,
∴AB=AF,
∴∠ABG=∠AFG=30°,
∴∠AGB=90°,
∴∠EGF=90°,
∴四边形GEHF是矩形;
即当x=2时,四边形GEHF是矩形.
点评 本题考查了平行四边形的判定与性质、等边三角形的判定与性质、矩形的判定;熟练掌握平行四边形的性质,并能进行推理论证是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.如图中,表示函数关系的是( )
| A. |  | B. |  | C. |  | D. |  |
18.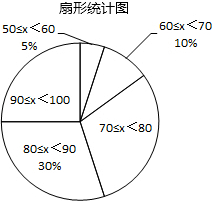 某校组织初中2000名学生游览参观“五大道”,并以此开展“五大道”历史经历知识竞赛活动,现从中随机抽取若干名学生的得分(满分100分,成绩均为正数)进行统计,整理出下列竞赛成绩统计表和扇形统计图(均不完整).
某校组织初中2000名学生游览参观“五大道”,并以此开展“五大道”历史经历知识竞赛活动,现从中随机抽取若干名学生的得分(满分100分,成绩均为正数)进行统计,整理出下列竞赛成绩统计表和扇形统计图(均不完整).
成绩统计表
如果成绩在90分以上(含90分)可获得一等奖;70分以上(含70分),90分以下的可获得二等奖;其余学生可获得鼓励奖,根据以上图表的数据解答下列问题:
(1)本次活动共随机抽取了多少名学生?
(2)估计本次活动获得二等奖的学生有多少名?
(3)绘制频数分布直方图.
 某校组织初中2000名学生游览参观“五大道”,并以此开展“五大道”历史经历知识竞赛活动,现从中随机抽取若干名学生的得分(满分100分,成绩均为正数)进行统计,整理出下列竞赛成绩统计表和扇形统计图(均不完整).
某校组织初中2000名学生游览参观“五大道”,并以此开展“五大道”历史经历知识竞赛活动,现从中随机抽取若干名学生的得分(满分100分,成绩均为正数)进行统计,整理出下列竞赛成绩统计表和扇形统计图(均不完整).成绩统计表
| 成绩x(分) | 频数(人) |
| 50≤x<60 | 10 |
| 60≤x<70 | 20 |
| 70≤x<80 | 60 |
| 80≤x<90 | 60 |
| 90≤x<100 | 50 |
(1)本次活动共随机抽取了多少名学生?
(2)估计本次活动获得二等奖的学生有多少名?
(3)绘制频数分布直方图.
15.给出下列四个命题,其中真命题是( )
| A. | 如果a2>0,那么a>0 | B. | 如果m是自然数,那么m是整数 | ||
| C. | 矩形的对角线互相垂直平分 | D. | 菱形的对角线相等 |
 如图,已知AB=AC,AD=AE,BD=EC,则图中有2对全等三角形,它们是△ABD≌△ACE,△ABE≌△ACD.
如图,已知AB=AC,AD=AE,BD=EC,则图中有2对全等三角形,它们是△ABD≌△ACE,△ABE≌△ACD.