题目内容
9.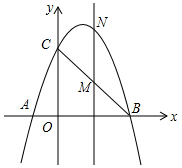 如图,二次函数y=ax2-2ax+3(a≠0)的图象与x、y轴交于A、B、C三点,
如图,二次函数y=ax2-2ax+3(a≠0)的图象与x、y轴交于A、B、C三点,其中AB=4,连接BC.
(1)求二次函数的对称轴和函数表达式;
(2)若点M是线段BC上的动点,设点M的横坐标为m,过点M作MN∥y轴交抛物线于点N,求线段MN的最大值;
(3)当0≤x≤t时,则3≤y≤4,直接写出t的取值范围.
分析 (1)根据对称轴x=1,AB=4,可得A(-1,0),B(3,0),利用待定系数法即可解决问题.
(2)由直线BC的解析式为y=-x+3,设M(m,-m+3),则N(m,-m2+2m+3),推出NM=-m2+2m+3-(-m+3)=-m2+3m=-(m-$\frac{3}{2}$)2+$\frac{9}{4}$,根据二次函数的性质即可解决问题.
(3)求出抛物线的顶点坐标,观察好像图象,即可解决问题.
解答 解:(1)∵二次函数解析式为y=ax2-2ax+3,
∴对称轴x=1,
∵AB=4,
∴A(-1,0),B(3,0),
把(-1,0)代入二次函数的解析式得到a=-1,
∴二次函数的解析式为y=-x2+2x+3.
(2)∵直线BC的解析式为y=-x+3,设M(m,-m+3),
则N(m,-m2+2m+3),
∴NM=-m2+2m+3-(-m+3)=-m2+3m=-(m-$\frac{3}{2}$)2+$\frac{9}{4}$,
∵-1<0,
∴m=$\frac{3}{2}$时,MN有最大值,最大值为$\frac{9}{4}$.
(3)∵y=-x2+2x+3=-(x-1)2+4,
∴顶点坐标(1,4),
∵y=3时3=-x2+2x+3,解得x=0或2,
∴0≤x≤t时,则3≤y≤4,
∴结合图象可知,1≤t≤2.
点评 本题考查二次函数与x轴的交点、待定系数法确定函数解析式等知识,解题的关键是熟练掌握待定系数法确定函数解析式,学会构建二次函数解决最值问题,属于中考常考题型.

练习册系列答案
相关题目
19.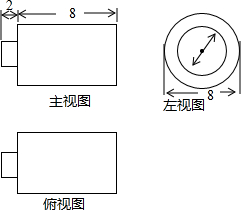 如图,是某几何体的三视图,根据图中所标的数据求得该几何体的体积为( )
如图,是某几何体的三视图,根据图中所标的数据求得该几何体的体积为( )
 如图,是某几何体的三视图,根据图中所标的数据求得该几何体的体积为( )
如图,是某几何体的三视图,根据图中所标的数据求得该几何体的体积为( )| A. | 120π | B. | 132π | C. | 136π | D. | 236π |
4.某校参加校园青春健身操比赛的16名运动员的身高如表:
则该校16名运动员身高的平均数和中位数分别是(单位:cm)( )
| 身高(cm) | 172 | 173 | 175 | 176 |
| 人数(个) | 2 | 7 | 3 | 4 |
| A. | 174cm,173cm | B. | 173cm,174cm | C. | 174cm,174cm | D. | 174cm,175cm |
1.下列计算错误的是( )
| A. | 3$\sqrt{2}$-$\sqrt{2}$=3 | B. | $\sqrt{60}$÷$\sqrt{5}$=2$\sqrt{3}$ | C. | $\sqrt{25a}$+$\sqrt{9a}$=8$\sqrt{a}$ | D. | $\sqrt{14}$×$\sqrt{7}$=7$\sqrt{2}$ |
 如图,小明在操场上从A点出发,沿直线前进5米后向左转40°,再沿直线前进5米后,又向左转40°,照这样走下去,他第一次回到出发地A点时,一共走了45米.
如图,小明在操场上从A点出发,沿直线前进5米后向左转40°,再沿直线前进5米后,又向左转40°,照这样走下去,他第一次回到出发地A点时,一共走了45米.