先化简.再求值:-a.其中a=-2.b=$\frac{1}{2}$,-32.其中a=-1.b=-3．题目和参考答案——青夏教育精英家教网—

题目内容

17．先化简，再求值：
（1）2（a+2）（b-4）-a（4a-3b），其中a=-2，b=$\frac{1}{2}$；
（2）（2a+b）（2a-b）-3（2a-b）²，其中a=-1，b=-3．

分析（1）原式利用多项式乘以多项式，以及单项式乘以多项式法则计算，去括号合并得到最简结果，把a与b的值代入计算即可求出值；
（2）原式利用平方差公式，以及完全平方公式化简，去括号合并得到最简结果，把a与b的值代入计算即可求出值．

解答解：（1）原式=2ab-8a+4b-16-4a²+3ab=-4a²+5ab-8a+4b-16，
当a=-2，b=$\frac{1}{2}$时，原式=-16-5+16+2-16=-19；

（2）原式=4a²-b²-12a²+12ab-3b²=-8a²+12ab-4b²，
当a=-1，b=-3时，原式=-8+36-36=-8．

点评此题考查了整式的混合运算-化简求值，熟练掌握公式及法则是解本题的关键．

练习册系列答案

黄冈重点中学名师编写金卷100分系列答案

相关题目

7．下列分式运算，正确的是（　　）

A．

（$\frac{3x}{5y}$）²=$\frac{3{x}^{2}}{5{y}^{2}}$

B．

$\frac{1}{x-y}-\frac{1}{y-x}$=0

C．

$\frac{1}{3x}+\frac{1}{3y}=\frac{1}{3（x+y）}$

D．

（$\frac{{x}^{2}}{-y}$）³=-$\frac{{x}^{6}}{{y}^{3}}$

8．（1）计算：（-1）²⁰¹⁷+|$\sqrt{3}$-3|+（tan30°）^-1
（2）解方程组：$\left\{\begin{array}{l}{x-y=5}\\{2x+y=4}\end{array}\right.$．

5．先化简，再求值：（2x+1）（2x-1）-3x（x+1）-（x-1）²，当x=-1．

12．计算：（-a）⁵•（a²）³÷（-a）⁴的结果，正确的是（　　）

-a⁷

-a⁶

a⁷

a⁶

2．

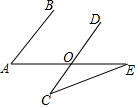如图，AB∥CD，∠C=35°，∠E=25°，则∠A=60°°．

9．

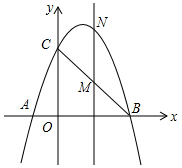如图，二次函数y=ax²-2ax+3（a≠0）的图象与x、y轴交于A、B、C三点，
其中AB=4，连接BC．
（1）求二次函数的对称轴和函数表达式；
（2）若点M是线段BC上的动点，设点M的横坐标为m，过点M作MN∥y轴交抛物线于点N，求线段MN的最大值；
（3）当0≤x≤t时，则3≤y≤4，直接写出t的取值范围．

6．若|x²-16|+$\sqrt{y-3}$=0，则x+y=7或-1．

7．分式$\frac{1}{x-1}$有意义，则x的值为（　　）

试题分类