题目内容
17.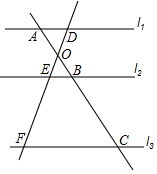 如图,已知l1∥l2∥l3,两条直线交于点O,且与这三条平行线分别交于点A、B、C和D、E、F,若AB=2,BC=3,BE=1,CF=4,求AO的长.
如图,已知l1∥l2∥l3,两条直线交于点O,且与这三条平行线分别交于点A、B、C和D、E、F,若AB=2,BC=3,BE=1,CF=4,求AO的长.
分析 先根据平行线分线段成比例定理,由l2∥l3得到$\frac{OB}{OC}$=$\frac{BE}{FC}$,则可计算出OB的长,然后计算AB-OB即可.
解答 解:∵l2∥l3,
∴$\frac{OB}{OC}$=$\frac{BE}{FC}$,即$\frac{OB}{OB+3}$=$\frac{1}{4}$,
∴OB=1,
∴AO=AB-OB=2-1=1.
点评 本题考查了平行线分线段成比例:三条平行线截两条直线,所得的对应线段成比例.平行于三角形的一边,并且和其他两边(或两边的延长线)相交的直线,所截得的三角形的三边与原三角形的三边对应成比例.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
7.下列等式不正确的是( )
| A. | (a2)3=a6 | B. | a2+a2=2a2 | C. | (3a)2=6a2 | D. | a6÷a2=a4 |
 已知:如图,AB∥DE,FE∥BC交AB于点F,∠E=120°,求∠B的度数.
已知:如图,AB∥DE,FE∥BC交AB于点F,∠E=120°,求∠B的度数. 小张对他所在学校的同学使用手机的情况进行了调查,并根据调查的结果制作了如图所示的统计图,由图可知,利用手机玩游戏的同学占30%,则利用手机上网学习的同学所在的扇形的圆心角的度数是72°.
小张对他所在学校的同学使用手机的情况进行了调查,并根据调查的结果制作了如图所示的统计图,由图可知,利用手机玩游戏的同学占30%,则利用手机上网学习的同学所在的扇形的圆心角的度数是72°.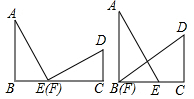 (1)以a,b为直角边,c为斜边作两个全等的Rt△ABE与Rt△FCD拼成如图1所示的图形,使B,E,F,C四点在一条直线上(此时E,F重合),可知△ABE≌△FCD,AE⊥DF,请你证明:a2+b2=c2;
(1)以a,b为直角边,c为斜边作两个全等的Rt△ABE与Rt△FCD拼成如图1所示的图形,使B,E,F,C四点在一条直线上(此时E,F重合),可知△ABE≌△FCD,AE⊥DF,请你证明:a2+b2=c2;