题目内容
1.已知$\left\{\begin{array}{l}{\frac{x}{2}=\frac{3y}{4}=\frac{2z}{5}}\\{x+3y+2z=22}\end{array}\right.$,则x=4,y=$\frac{8}{3}$,z=5.分析 设$\frac{x}{2}$=$\frac{3y}{4}$=$\frac{2z}{5}$=k,得出x=2k,y=$\frac{4}{3}$k,z=$\frac{5}{2}$k,进一步代入x+3y+2z=22求得k,代入求得x、y、z即可.
解答 解:$\left\{\begin{array}{l}{\frac{x}{2}=\frac{3y}{4}=\frac{2z}{5}}\\{x+3y+2z=22}\end{array}\right.$,
设$\frac{x}{2}$=$\frac{3y}{4}$=$\frac{2z}{5}$=k,则x=2k,y=$\frac{4}{3}$k,z=$\frac{5}{2}$k,
代入x+3y+2z=22得
2k+4k+5k=22
解得:k=2,
因此x=4,y=$\frac{8}{3}$,z=5.
故答案为:4,$\frac{8}{3}$,5.
点评 此题考查解三元一次方程组,设出参数,表示出三个未知数代入消元是解决问题的关键.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
11.3.14-π的相反数为( )
| A. | 0 | B. | 3.14-π | C. | π-3.14 | D. | 0.14 |
12.下列条件能让两个三角形全等的是( )
| A. | 有一边和两角对应相等 | B. | 有两边和一角对应相等 | ||
| C. | 三个角对应相等 | D. | 面积相等且有一边相等 |
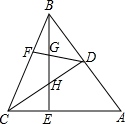 如图,在△ABC中,∠ABC=45°,CD⊥AB,BE⊥AC,垂足分别为D,E,F为BC中点,BE与DF,DC分别交于点G,H,∠ABE=∠CBE,AC=6cm.
如图,在△ABC中,∠ABC=45°,CD⊥AB,BE⊥AC,垂足分别为D,E,F为BC中点,BE与DF,DC分别交于点G,H,∠ABE=∠CBE,AC=6cm.