题目内容
4.计算:($\sqrt{24}$+$\sqrt{\frac{1}{6}}$)×$\sqrt{6}$=13.分析 先把各二次根式化简为最简二次根式,然后把括号内合并后进行二次根式的乘法运算即可.
解答 解:原式=(2$\sqrt{6}$+$\frac{\sqrt{6}}{6}$)×$\sqrt{6}$
=$\frac{13\sqrt{6}}{6}$×$\sqrt{6}$
=13.
故答案为13.
点评 本题考查了二次根式的混合运算:先把各二次根式化简为最简二次根式,然后进行二次根式的乘除运算,再合并即可.

练习册系列答案
相关题目
15.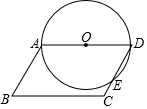 如图,?ABCD中,∠B=70°,BC=6,以AD为直径的⊙O交CD于点E,则$\widehat{DE}$的长为( )
如图,?ABCD中,∠B=70°,BC=6,以AD为直径的⊙O交CD于点E,则$\widehat{DE}$的长为( )
 如图,?ABCD中,∠B=70°,BC=6,以AD为直径的⊙O交CD于点E,则$\widehat{DE}$的长为( )
如图,?ABCD中,∠B=70°,BC=6,以AD为直径的⊙O交CD于点E,则$\widehat{DE}$的长为( )| A. | $\frac{1}{3}$π | B. | $\frac{2}{3}$π | C. | $\frac{7}{6}$π | D. | $\frac{4}{3}$π |
19.计算6m6÷(-2m2)3的结果为( )
| A. | -m | B. | -1 | C. | $\frac{3}{4}$ | D. | -$\frac{3}{4}$ |
16.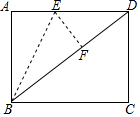 如图,在矩形ABCD中BC=8,CD=6,将△ABE沿BE折叠,使点A恰好落在对角线BD上F处,则DE的长是( )
如图,在矩形ABCD中BC=8,CD=6,将△ABE沿BE折叠,使点A恰好落在对角线BD上F处,则DE的长是( )
 如图,在矩形ABCD中BC=8,CD=6,将△ABE沿BE折叠,使点A恰好落在对角线BD上F处,则DE的长是( )
如图,在矩形ABCD中BC=8,CD=6,将△ABE沿BE折叠,使点A恰好落在对角线BD上F处,则DE的长是( )| A. | 3 | B. | $\frac{24}{5}$ | C. | 5 | D. | $\frac{89}{16}$ |
6.下列各题变形正确的是( )
| A. | 3(x+8)=3x+8 | B. | 6x+5=6(x+5) | C. | -(x-6)=x-6 | D. | -a+b=-(a-b) |
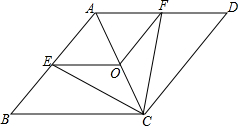 已知:如图,在菱形ABCD中,点E,O,F分别为AB,AC,AD的中点,连接CE,CF,OE,OF.
已知:如图,在菱形ABCD中,点E,O,F分别为AB,AC,AD的中点,连接CE,CF,OE,OF.