题目内容
20.某种商品,平均每天可销售20件,每件盈利44元,若此商品每降价1元,则每天可多售5件,设每件商品降价x元,则每件盈利y元.(1)写出y与x的函数关系式;
(2)每件降价多少元时,每天盈利最多,最多是多少?此时的销售量为多少?
分析 (1)由每件应降价x元,获得的利润为y元,每件降价1元,则每天可多售5件表示出每件的利润及卖的件数,根据总利润=每件的利润×卖的件数列出y与x的函数;
(2)对于(1)中的函数关系式整理配方后,利用二次函数的性质即可得到最大利润及此时每件应将的钱数.
解答 解:由每件应降价x元,获得的利润为y元,
根据题意得:y=(44-x)(20+5x),
即y与x的函数关系式为:y=-5x2+200x+880;
(2)∵y=-5x2+200x+880配方得:y=-5(x-20)2+2880,
∴当x=20时,y有最大值且最大值为2880元.
答:每件应降价20元,最大利润为2880元.
点评 此题考查了二次函数的应用,其中根据每件降价1元,则每天可多售5件表示出每件的利润及卖的件数是列函数解析式的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
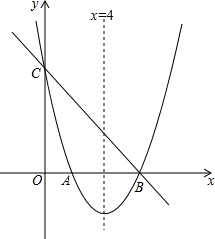 如图所示,抛物线y=ax2+bx+c与直线y=-x+6分别交于x轴和y轴上同一点,交点分别是点B和点C,且抛物线的对称轴为直线x=4.
如图所示,抛物线y=ax2+bx+c与直线y=-x+6分别交于x轴和y轴上同一点,交点分别是点B和点C,且抛物线的对称轴为直线x=4. 如图所示,根据所给条件,判断△ABC和△DBE是否相似,并说明理由.
如图所示,根据所给条件,判断△ABC和△DBE是否相似,并说明理由. 如图,五边形ABCDE与五边形A′B′C′D′E′位似,对应边CD=2,C′D′=3,则AB:A′B′=2:3.
如图,五边形ABCDE与五边形A′B′C′D′E′位似,对应边CD=2,C′D′=3,则AB:A′B′=2:3.