题目内容
11.已知抛物线y=x2-mx+2m-4.(1)求证:不论m为何实数,抛物线总与x轴有交点;
(2)当抛物线与x轴交于A、B两点(点A在y轴左侧,点B在y轴右侧),且OA与OB的比为2:1时,求m的值.
分析 (1)先计算判别式的值,再利用非负数的性质判断△≥0,然后根据△=b2-4ac决定抛物线与x轴的交点个数可判断不论m为何实数,抛物线总与x轴有交点;
(2)设A(-2t,0),B(t,0),(t>0),利用交点式得到y=(x+2t)(x-t)=x2+tx-2t2,于是-m=t,2m-4=-2t2,消去t得到2m-4=-2m2,解得m1=-2,m2=1,然后利用t=-m>0可确定m的值.
解答 (1)证明:△=(-m)2-4(2m-4)
=m2-8m+126
=(m-4)2,
∵(m-4)2≥0,即△≥0,
∴不论m为何实数,抛物线总与x轴有交点;
(2)解:设A(-2t,0),B(t,0),(t>0),
则y=(x+2t)(x-t)=x2+tx-2t2,
所以-m=t,2m-4=-2t2,
所以2m-4=-2m2,
整理得m2+m-2=0,解得m1=-2,m2=1,
而t=-m>0,
所以m的值为-2.
点评 本题考查了抛物线与x轴的交点:把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标转化为解关于x的一元二次方程;△=b2-4ac决定抛物线与x轴的交点个数:△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.

练习册系列答案
相关题目
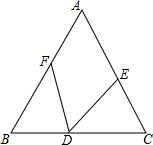 如图,在△ABC中,已知AB=AC,D为BC上一点,BF=CD,CE=BD,求证:∠EDF=90°-$\frac{1}{2}$∠A.
如图,在△ABC中,已知AB=AC,D为BC上一点,BF=CD,CE=BD,求证:∠EDF=90°-$\frac{1}{2}$∠A. 如图,已知∠AOB=100°,OD平分∠BOC,OF平分∠AOC,求△DOF的度数.
如图,已知∠AOB=100°,OD平分∠BOC,OF平分∠AOC,求△DOF的度数.