题目内容
 如图,取一张长方形纸片,按图中所示的方法折叠一角,得到折痕PO,再折叠一角,得到折痕QO,如果两折痕的夹角∠POQ=70°,则∠AOB=
如图,取一张长方形纸片,按图中所示的方法折叠一角,得到折痕PO,再折叠一角,得到折痕QO,如果两折痕的夹角∠POQ=70°,则∠AOB=考点:角的计算,翻折变换(折叠问题)
专题:
分析:由折叠的性质可得∠A′OP=∠AOP=45°,由∠POQ=70°,可得∠A′OQ=25°,进而得出∠PQO=65°,由DC∥AB,可得∠QOB=∠PQO=65°,然后由折叠的性质可知∠B′OQ=∠BOQ=65°,所以∠AOB=∠A′OB′=∠B′OQ-∠A′OQ=65°-25°=40°
解答:解:由折叠的性质可得∠A′OP=∠AOP,∠B′OQ=∠BOQ,
∵∠POQ=∠POA′+∠A′OQ,∠POQ=70°,
∴∠A′OQ=∠POQ-∠POA′,
∵∠PQO=90°-∠A′OQ,DC∥AB,
∴∠QOB=∠PQO,
∴∠B′OQ=∠BOQ,
∴∠A′OB′=∠B′OQ-∠A′OQ=2(90°-70°)=40°,
∴∠AOB=40°.
故答案为:40
∵∠POQ=∠POA′+∠A′OQ,∠POQ=70°,
∴∠A′OQ=∠POQ-∠POA′,
∵∠PQO=90°-∠A′OQ,DC∥AB,
∴∠QOB=∠PQO,
∴∠B′OQ=∠BOQ,
∴∠A′OB′=∠B′OQ-∠A′OQ=2(90°-70°)=40°,
∴∠AOB=40°.
故答案为:40
点评:此题考查了折叠问题中角的计算,解题的关键是:明确折叠前后两个图形全等,对应角相等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
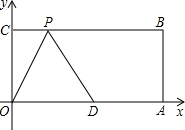 如图,四边形OABC是矩形,点A、C的坐标分别为A(10,0),C(0,4),点D是OA的中点,点P在BC边上运动.当△ODP是腰长为5的等腰三角形时,点P的坐标为
如图,四边形OABC是矩形,点A、C的坐标分别为A(10,0),C(0,4),点D是OA的中点,点P在BC边上运动.当△ODP是腰长为5的等腰三角形时,点P的坐标为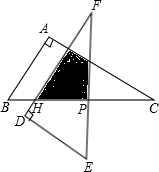 如图,△ABC中,∠A=90°,∠C=30°,BC=12cm,把△ABC绕着它的斜边中点P逆时针旋转90°至△DEF的位置,DF交BC于点H.△ABC与△DEF重叠部分的面积为
如图,△ABC中,∠A=90°,∠C=30°,BC=12cm,把△ABC绕着它的斜边中点P逆时针旋转90°至△DEF的位置,DF交BC于点H.△ABC与△DEF重叠部分的面积为 如图,在等边△ABC中,∠ABC与∠ACB的平分线相交于点O,且OD∥AB,OE∥AC
如图,在等边△ABC中,∠ABC与∠ACB的平分线相交于点O,且OD∥AB,OE∥AC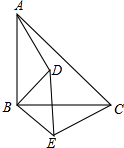 已知:如图,△ABC和△DBE均为等腰直角三角形.
已知:如图,△ABC和△DBE均为等腰直角三角形.