题目内容
7. 如图,菱形ABCD的两条对角线AC,BD相交于点O,若AC=4,BD=6,则菱形ABCD的周长为( )
如图,菱形ABCD的两条对角线AC,BD相交于点O,若AC=4,BD=6,则菱形ABCD的周长为( )| A. | 16 | B. | 24 | C. | 4$\sqrt{13}$ | D. | 8$\sqrt{13}$ |
分析 根据菱形对角线互相垂直平分的性质,可以求得BO=OD,AO=OC,在Rt△AOD中,根据勾股定理可以求得AB的长,即可求得菱形ABCD的周长.
解答 解:∵四边形ABCD是菱形,
∴BO=OD=$\frac{1}{2}$AC=2,AO=OC=$\frac{1}{2}$BD=3,AC⊥BD,
∴AB=$\sqrt{A{O}^{2}+B{O}^{2}}$=$\sqrt{13}$,
∴菱形的周长为4$\sqrt{13}$.
故选:C.
点评 本题考查了勾股定理在直角三角形中的运用,考查了菱形各边长相等的性质,本题中根据勾股定理计算AB的长是解题的关键.

练习册系列答案
 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
18.不等式1-2x<1 的解集是( )
| A. | x>-1 | B. | x<-1 | C. | x>1 | D. | x>0 |
15. 如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若矩形的面积为16$\sqrt{3}$,AE=B′D,∠EFB=60°,则线段DE的长是( )
如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若矩形的面积为16$\sqrt{3}$,AE=B′D,∠EFB=60°,则线段DE的长是( )
 如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若矩形的面积为16$\sqrt{3}$,AE=B′D,∠EFB=60°,则线段DE的长是( )
如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若矩形的面积为16$\sqrt{3}$,AE=B′D,∠EFB=60°,则线段DE的长是( )| A. | 4$\sqrt{3}$ | B. | 5 | C. | 6 | D. | 6$\sqrt{3}$ |
 如图,∠BAF=40°,∠ACE=130°,CE⊥CD.问CD∥AB吗?为什么?
如图,∠BAF=40°,∠ACE=130°,CE⊥CD.问CD∥AB吗?为什么?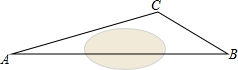 在一次课外实践活动中,同学们要测量某公园人工湖两侧A,B两个凉亭之间的距离.如图,现测得∠ABC=30°,∠CAB=15°,AC=200米,请计算A,B两个凉亭之间的距离(结果精确到1米)(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
在一次课外实践活动中,同学们要测量某公园人工湖两侧A,B两个凉亭之间的距离.如图,现测得∠ABC=30°,∠CAB=15°,AC=200米,请计算A,B两个凉亭之间的距离(结果精确到1米)(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)