题目内容
10.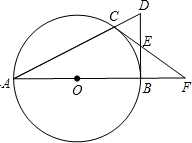 如图,点C是以AB为直径的圆O上一点,直线AC与过B点的切线相交于D,点E是BD的中点,直线CE交直线AB于点F.
如图,点C是以AB为直径的圆O上一点,直线AC与过B点的切线相交于D,点E是BD的中点,直线CE交直线AB于点F.(1)求证:CF是⊙O的切线;
(2)若ED=3,EF=5,求⊙O的半径.
分析 (1)连CB、OC,根据切线的性质得∠ABD=90°,根据圆周角定理由AB是直径得到∠ACB=90°,即∠BCD=90°,则根据直角三角形斜边上的中线性质得CE=BE,于是得到∠OBC+∠CBE=∠OCB+∠BCE=90°,然后根据切线的判定定理得CF是⊙O的切线;
(2)CE=BE=DE=3,于是得到CF=CE+EF=4,然后根据相似三角形的性质即可得到结论.
解答 (1)证明:连CB、OC,如图,
∵BD为⊙O的切线,
∴DB⊥AB,
∴∠ABD=90°,
∵AB是直径,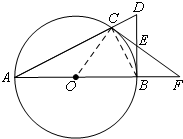
∴∠ACB=90°,
∴∠BCD=90°,
∵E为BD的中点,
∴CE=BE,
∴∠BCE=∠CBE,
而∠OCB=∠OBC,
∴∠OBC+∠CBE=∠OCB+∠BCE=90°,
∴OC⊥CF,
∴CF是⊙O的切线;
(2)解:CE=BE=DE=3,
∵EF=5,
∴CF=CE+EF=8,
∵∠ABD=90°,
∴∠EBF=90°,
∵∠OCF=90°,
∴∠EBF=∠OCF,
∵∠F=∠F,
∴△EBF∽△OCF,
∴$\frac{BE}{BF}=\frac{OC}{CF}$,
∴$\frac{3}{4}=\frac{OC}{8}$,
∴OC=6,
即⊙O的半径为6.
点评 本题考查了切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.也考查了勾股定理、圆周角定理.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.下列说法中,不正确的是( )
| A. | 经过直线外一点,有且只有一条直线与这条直线平行 | |
| B. | 在同一平面内,垂直于同一条直线的两条直线互相平行 | |
| C. | 如果∠1与∠2是同位角,那么∠1=∠2 | |
| D. | 平移不改变图形的形状和大小 |
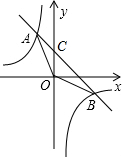 如图,已知一次函数y=kx+b的图象与反比例函数y=-$\frac{8}{x}$的图象交于A、B两点,且点A的横坐标与点B的纵坐标都是-2.
如图,已知一次函数y=kx+b的图象与反比例函数y=-$\frac{8}{x}$的图象交于A、B两点,且点A的横坐标与点B的纵坐标都是-2.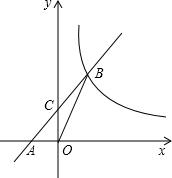 如图,在平面直角坐标系中,直线y=k1x+2与x轴交于点A,与y轴交于点C,与反比例函数y=$\frac{{k}_{2}}{x}$在第一象限内的图象交于点B,连接BO,若S△OBC=1,tan∠BOC=$\frac{1}{3}$,求k2的值.
如图,在平面直角坐标系中,直线y=k1x+2与x轴交于点A,与y轴交于点C,与反比例函数y=$\frac{{k}_{2}}{x}$在第一象限内的图象交于点B,连接BO,若S△OBC=1,tan∠BOC=$\frac{1}{3}$,求k2的值.
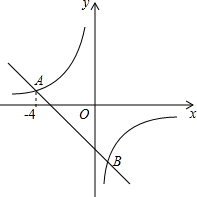 在平面直角坐标系xOy中,一次函数y=-x+k的图象与反比例函数y=-$\frac{4}{x}$的图象交于点A(-4,n)和点B.
在平面直角坐标系xOy中,一次函数y=-x+k的图象与反比例函数y=-$\frac{4}{x}$的图象交于点A(-4,n)和点B. 如图,正方形网格中的每个小正方形边长都是1,任意连结这些小正方形的顶点,可得到一些线段,请在图中画出△ABC,使得AB=5,AC=$\sqrt{10}$,BC=$\sqrt{17}$,并求出此三角形的面积.
如图,正方形网格中的每个小正方形边长都是1,任意连结这些小正方形的顶点,可得到一些线段,请在图中画出△ABC,使得AB=5,AC=$\sqrt{10}$,BC=$\sqrt{17}$,并求出此三角形的面积.