题目内容
2.两地相距s千米,回来时车速比去时提高了50%,因而回来比去时途中时间缩短了t小时.(1)回来时的速度是去时的速度的$\frac{3}{2}$倍;
(2)用含s、t的式子表示去时的速度.
分析 (1)根据回来时车速比去时提高了50%,可得回来时的速度=去时的速度×(1+50%),进而求解即可;
(2)设去时的速度是x千米/时,则回来的速度是$\frac{3}{2}$x千米/时,根据回来比去时途中时间缩短了t小时建立方程,求解即可.
解答 解:(1)由题意得,回来时的速度:去时的速度=$\frac{3}{2}$.
故答案为$\frac{3}{2}$;
(2)设去时的速度是x千米/时,则回来的速度是$\frac{3}{2}$x千米/时.
由题意,得$\frac{s}{x}$-$\frac{s}{\frac{3}{2}x}$=t,
解得,x=$\frac{s}{3t}$.
经检验,x=$\frac{s}{3t}$是原方程的解且符合题意.
答:去时的速度是$\frac{s}{3t}$千米/时.
点评 本题考查分式方程的应用,分析题意,找到合适的等量关系是解决问题的关键.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
4.某市2014年1月21日至24日每天的最高气温与最低气温如表:
其中温差最大的一天是( )
| 日期 | 1月21日 | 1月22日 | 1月23日 | 1月24日 |
| 最高气温 | 8℃ | 7℃ | 5℃ | 6℃ |
| 最低气温 | -3℃ | -5℃ | -4℃ | -2℃ |
| A. | 1月21日 | B. | 1月22日 | C. | 1月23日 | D. | 1月24日 |
7. 如图,下面是利用尺规作∠AOB的角平分线OC的作法:
如图,下面是利用尺规作∠AOB的角平分线OC的作法:
①以点O为圆心,任意长为半径作弧,交OA、OB于点D,E;
②分别以点D,E为圆心,以大于$\frac{1}{2}$DE的长为半径作弧,两弧在∠AOB内部交于点C;
③作射线OC,则射线OC就是∠AOB的平分线.
以上用尺规作角平分线时,用到的三角形全等的判定方法是( )
 如图,下面是利用尺规作∠AOB的角平分线OC的作法:
如图,下面是利用尺规作∠AOB的角平分线OC的作法:①以点O为圆心,任意长为半径作弧,交OA、OB于点D,E;
②分别以点D,E为圆心,以大于$\frac{1}{2}$DE的长为半径作弧,两弧在∠AOB内部交于点C;
③作射线OC,则射线OC就是∠AOB的平分线.
以上用尺规作角平分线时,用到的三角形全等的判定方法是( )
| A. | SSS | B. | SAS | C. | ASA | D. | AAS |
14. 一名工作人员不慎将一块三角形模具打碎成了三块,如图所示,他是否可以只带其中的一块碎片到商店去,就能买一块与原来一模一样的三角形模具呢?答案是肯定的,那么他该带哪款去?( )
一名工作人员不慎将一块三角形模具打碎成了三块,如图所示,他是否可以只带其中的一块碎片到商店去,就能买一块与原来一模一样的三角形模具呢?答案是肯定的,那么他该带哪款去?( )
 一名工作人员不慎将一块三角形模具打碎成了三块,如图所示,他是否可以只带其中的一块碎片到商店去,就能买一块与原来一模一样的三角形模具呢?答案是肯定的,那么他该带哪款去?( )
一名工作人员不慎将一块三角形模具打碎成了三块,如图所示,他是否可以只带其中的一块碎片到商店去,就能买一块与原来一模一样的三角形模具呢?答案是肯定的,那么他该带哪款去?( )| A. | 不能 | B. | 带① | C. | 带② | D. | 带③ |
11.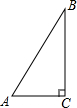 如图,在△ABC中,∠C=90°,sinA=$\frac{4}{5}$,BC=12,则AC=( )
如图,在△ABC中,∠C=90°,sinA=$\frac{4}{5}$,BC=12,则AC=( )
 如图,在△ABC中,∠C=90°,sinA=$\frac{4}{5}$,BC=12,则AC=( )
如图,在△ABC中,∠C=90°,sinA=$\frac{4}{5}$,BC=12,则AC=( )| A. | 3 | B. | 9 | C. | 10 | D. | 15 |
 已知:AB⊥AC,AD⊥AE,且AB=AC,AD=AE,求证:
已知:AB⊥AC,AD⊥AE,且AB=AC,AD=AE,求证: 如图所示,在△ABC中,∠BAC=90°,AB=AC,DE过A点,且CE⊥ED,BD⊥ED.若CE=2,BD=4,求ED的长.
如图所示,在△ABC中,∠BAC=90°,AB=AC,DE过A点,且CE⊥ED,BD⊥ED.若CE=2,BD=4,求ED的长.