题目内容
7.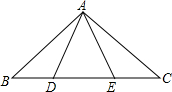 已知如图,在△ABC中,AB=AC,D、E是BC上异于B、C的任意两点,连接AD和AE,且AD=AE.
已知如图,在△ABC中,AB=AC,D、E是BC上异于B、C的任意两点,连接AD和AE,且AD=AE.(1)图中有几组全等三角形?请分别写出来;
(2)选择其中的一组证明两三角形全等.
分析 (1)根据全等三角形的判定进行解答即可;
(2)由AB=AC,利用等边对等角得到一对角相等,同理由AD=AE得到一对角相等,再利用外角性质及等量代换可得出一对角相等,利用ASA得出三角形ABD与三角形AEC全等,利用全等三角形的对应边相等可得证.
解答 解:(1)有2组全等三角形,分别是:△ABD≌△ACE;△ABE≌△ACD;
(2)∵AB=AC,
∴∠B=∠C(等边对等角),
∵AD=AE,
∴∠ADE=∠AED(等边对等角),
又∠ADE=∠B+∠BAD,∠AED=∠C+∠CAE,
∴∠BAD=∠CAE(等量代换),
在△ABD和△ACE中,
$\left\{\begin{array}{l}{∠B=∠C}\\{AB=AC}\\{∠BAD=∠CAE}\end{array}\right.$,
∴△ABD≌△ACE(ASA),
∴BD=CE(全等三角形的对应边相等).
点评 此题考查了全等三角形的判定与性质,等腰三角形的性质,利用了等量代换的思想,做题时注意一题多解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2.京津冀一体化协同发展是党中央的一项重大战略决策,它涉及到的国土面积约为120 000平方公里,人口总数约为90 000 000人.将90 000 000用科学记数法表示结果为( )
| A. | 9×106 | B. | 90×106 | C. | 9×107 | D. | 0.9×108 |




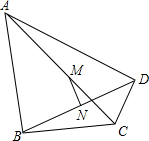 已知,如图,∠ABC=∠ADC=90°,M、N分别是AC、BD的中点.
已知,如图,∠ABC=∠ADC=90°,M、N分别是AC、BD的中点.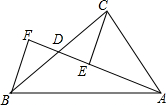 如图,AD是△ABC的中线,E、F分别是AD及AD延长线上的点,且DE=DF,连接BF、CE.则下列结论中正确的有( )
如图,AD是△ABC的中线,E、F分别是AD及AD延长线上的点,且DE=DF,连接BF、CE.则下列结论中正确的有( ) 如图所示,A B、C是一条公路边的三个村庄,A、B间的距离为100km,A、C间的距离为40km,现要从A、B之间设一个车站P,设P、C的距离为xkm;
如图所示,A B、C是一条公路边的三个村庄,A、B间的距离为100km,A、C间的距离为40km,现要从A、B之间设一个车站P,设P、C的距离为xkm; 如图,AB∥CD,∠A=110°,CE平分∠ACD,则∠ECD=35°.
如图,AB∥CD,∠A=110°,CE平分∠ACD,则∠ECD=35°.