题目内容
3.计算:($\sqrt{5}$+1)0+(-1)2015+$\sqrt{2}$sin45°-($\frac{1}{3}$)-1.分析 原式第一项利用零指数幂法则计算,第二项利用乘方的意义计算,第三项利用特殊角的三角函数值计算,最后一项利用负整数指数幂法则计算即可得到结果.
解答 解:原式=1-1+1-3
=-2.
点评 此题考查了实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
14.下列各式中,计算结果等于0的是( )
| A. | (-2)2-(-22) | B. | -22-22 | C. | -22+(-2)2 | D. | -22-(-2)2 |
18.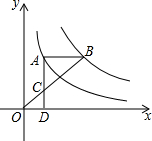 如图,点A在双曲线y=$\frac{3}{x}$上,点B在双曲线y=$\frac{k}{x}$(k≠0)上,AB∥x轴,过点A作AD⊥x轴于D.连接OB,与AD相交于点C,若AC=2CD,则k的值为( )
如图,点A在双曲线y=$\frac{3}{x}$上,点B在双曲线y=$\frac{k}{x}$(k≠0)上,AB∥x轴,过点A作AD⊥x轴于D.连接OB,与AD相交于点C,若AC=2CD,则k的值为( )
 如图,点A在双曲线y=$\frac{3}{x}$上,点B在双曲线y=$\frac{k}{x}$(k≠0)上,AB∥x轴,过点A作AD⊥x轴于D.连接OB,与AD相交于点C,若AC=2CD,则k的值为( )
如图,点A在双曲线y=$\frac{3}{x}$上,点B在双曲线y=$\frac{k}{x}$(k≠0)上,AB∥x轴,过点A作AD⊥x轴于D.连接OB,与AD相交于点C,若AC=2CD,则k的值为( )| A. | 6 | B. | 9 | C. | 10 | D. | 12 |
15. 如图,OP=1,过P作PP1⊥OP且PP1=1,得OP1=$\sqrt{2}$;再过P1作P1P2⊥OP1且P1P2=1,得OP2=$\sqrt{3}$;又过P2作P2P3⊥OP2且P2P3⊥OP2且P2P3=1,得OP3=2,;…依次法继续作下去,则OP2015长为( )
如图,OP=1,过P作PP1⊥OP且PP1=1,得OP1=$\sqrt{2}$;再过P1作P1P2⊥OP1且P1P2=1,得OP2=$\sqrt{3}$;又过P2作P2P3⊥OP2且P2P3⊥OP2且P2P3=1,得OP3=2,;…依次法继续作下去,则OP2015长为( )
 如图,OP=1,过P作PP1⊥OP且PP1=1,得OP1=$\sqrt{2}$;再过P1作P1P2⊥OP1且P1P2=1,得OP2=$\sqrt{3}$;又过P2作P2P3⊥OP2且P2P3⊥OP2且P2P3=1,得OP3=2,;…依次法继续作下去,则OP2015长为( )
如图,OP=1,过P作PP1⊥OP且PP1=1,得OP1=$\sqrt{2}$;再过P1作P1P2⊥OP1且P1P2=1,得OP2=$\sqrt{3}$;又过P2作P2P3⊥OP2且P2P3⊥OP2且P2P3=1,得OP3=2,;…依次法继续作下去,则OP2015长为( )| A. | 2015 | B. | 2016 | C. | $\sqrt{2015}$ | D. | $\sqrt{2016}$ |
13.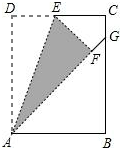 如图,在矩形ABCD中,点E是边CD的中点,将△ADE沿AE折叠后得到△AFE,且点F在矩形ABCD内部.将AF延长交边BC于点G.若$\frac{CG}{GB}$=$\frac{1}{8}$,则$\frac{AD}{AB}$是( )
如图,在矩形ABCD中,点E是边CD的中点,将△ADE沿AE折叠后得到△AFE,且点F在矩形ABCD内部.将AF延长交边BC于点G.若$\frac{CG}{GB}$=$\frac{1}{8}$,则$\frac{AD}{AB}$是( )
 如图,在矩形ABCD中,点E是边CD的中点,将△ADE沿AE折叠后得到△AFE,且点F在矩形ABCD内部.将AF延长交边BC于点G.若$\frac{CG}{GB}$=$\frac{1}{8}$,则$\frac{AD}{AB}$是( )
如图,在矩形ABCD中,点E是边CD的中点,将△ADE沿AE折叠后得到△AFE,且点F在矩形ABCD内部.将AF延长交边BC于点G.若$\frac{CG}{GB}$=$\frac{1}{8}$,则$\frac{AD}{AB}$是( )| A. | $\frac{4}{3}$ | B. | $\frac{3}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{3}$ |
 如图,在边长为1的网格中建立平面直角坐标系xOy,O、A、B三点均为格点.
如图,在边长为1的网格中建立平面直角坐标系xOy,O、A、B三点均为格点.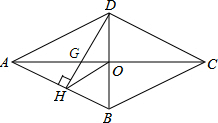 如图,四边形ABCD是菱形,对角线AC,BD相交于点O,过点D作DH丄AB于H,交AO于G,连接0H.
如图,四边形ABCD是菱形,对角线AC,BD相交于点O,过点D作DH丄AB于H,交AO于G,连接0H.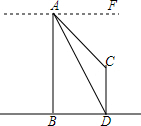 随着科技的发展,无人机现在已经有了更加广泛的应用,如图所示,一测绘机利用无人机测量某电视塔的高度.某一时刻,无人机的高度AB=500米,无人机此时在A处测得电视塔顶端C和底端D的俯角分别为45°和60°,求电视塔的高度.
随着科技的发展,无人机现在已经有了更加广泛的应用,如图所示,一测绘机利用无人机测量某电视塔的高度.某一时刻,无人机的高度AB=500米,无人机此时在A处测得电视塔顶端C和底端D的俯角分别为45°和60°,求电视塔的高度.