题目内容
18．一个不透明的盒子中装6个小球（除了颜色外无其他差别），从中随机抽取一个小球，共有3种可能的情况：红球、黄球和绿球，则随机摸出一球是红球的概率为（ ）| A． | $\frac{1}{6}$ | B． | $\frac{1}{2}$ | C． | $\frac{1}{3}$ | D． | 无法确定 |
分析 由于取到红球、黄球、绿球的可能性不等，于是不能确定随机摸出一球是红球的概率．
解答 解：从中随机抽取一个小球，共有3种可能的情况：红球、黄球和绿球，但它们发生的可能性不等，即红球、黄球和绿球的个数不确定，
所以随机摸出一球是红球的概率不确定．
故选D．
点评 本题考查了列表法与树状图法：利用列表法和树状图法展示所有可能的结果求出n，再从中选出符合事件A或B的结果数目m，求出概率．
练习册系列答案
相关题目
8．如表：方程1、方程2、方程3…是按照一定规律排列的一列方程：
（1）若方程$\frac{a}{x}$-$\frac{1}{x-b}$=1（a＞b）的解是x1=6，x2=10，则a=12b=5．
（2）请写出这列方程中第n个方程：$\frac{2n+4}{x}-\frac{1}{x-（n+1）}=1$ 方程的解：x1=n+2，x2=2n+2．
| 序号 | 方程 | 方程的解 |
| 1 | $\frac{6}{x}$-$\frac{1}{x-2}$=1 | x1=3，x2=4 |
| 2 | $\frac{8}{x}$-$\frac{1}{x-3}$=1 | x1=4，x2=6 |
| 3 | $\frac{10}{x}$-$\frac{1}{x-4}$=1 | x1=5，x2=8 |
| … | … | … |
（2）请写出这列方程中第n个方程：$\frac{2n+4}{x}-\frac{1}{x-（n+1）}=1$ 方程的解：x1=n+2，x2=2n+2．
6．
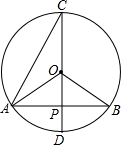如图，⊙O中，CD是直径，且CD⊥AB于P，则下列结论中不一定正确的是（ ）
如图，⊙O中，CD是直径，且CD⊥AB于P，则下列结论中不一定正确的是（ ）| A． | AP=PB | B． | $\widehat{AD}$=$\widehat{BD}$ | C． | ∠AOB=4∠ACD | D． | PO=PD |
3．设x是有理数，那么下列各式中一定表示正数的是（ ）
| A． | 2008x | B． | x+2008 | C． | |2008x| | D． | |x|+2008 |
8．下列图案均是用长度相同的小木棒按一定的规律拼搭而成的：拼搭第1个图案需4根小木棒，拼搭第2个图案需16根小木棒，…，依此规律拼成第7个图案需小木棒（ ）
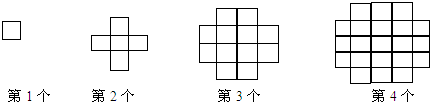
| A． | 76根 | B． | 104根 | C． | 136根 | D． | 144根 |