题目内容
13.若一直角三角形的两边长分别为8cm和15cm,则面积60或4$\sqrt{161}$cm.分析 按15为所给三角形的直角边和斜边,运用勾股定理来分类讨论、解析,即可解决问题.
解答 解:分两种情况:
①若8cm和15cm均为该直角三角形的两直角边时,
三角形的面积=$\frac{1}{2}$×8×15=60(cm2);
②若15为该直角三角形的斜边,
则另一条直角边长=$\sqrt{1{5}^{2}-{8}^{2}}$=$\sqrt{161}$(cm),
则三角形的面积=$\frac{1}{2}$×8×$\sqrt{161}$=4$\sqrt{161}$;
故答案为:60或4$\sqrt{161}$.
点评 该题主要考查了勾股定理及其应用问题;解题的关键是运用分类讨论的数学思想按15为直角边或斜边来分类讨论,逐一解析.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1. 如图,△ABC中,DE∥BC,DE=2,AD=4,DB=6,则BC的长是( )
如图,△ABC中,DE∥BC,DE=2,AD=4,DB=6,则BC的长是( )
 如图,△ABC中,DE∥BC,DE=2,AD=4,DB=6,则BC的长是( )
如图,△ABC中,DE∥BC,DE=2,AD=4,DB=6,则BC的长是( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
18.一个不透明的盒子中装6个小球(除了颜色外无其他差别),从中随机抽取一个小球,共有3种可能的情况:红球、黄球和绿球,则随机摸出一球是红球的概率为( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | 无法确定 |
 如图的截面形状是长方形.
如图的截面形状是长方形. 如图是正方体的展开图,原正方体相对两个面上的数字互为倒数,则a+c=-4.5.
如图是正方体的展开图,原正方体相对两个面上的数字互为倒数,则a+c=-4.5.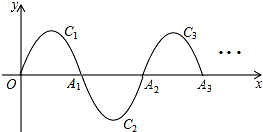 一段抛物线y=-x(x-3),(0≤x>3),记为C1,它与x轴交于点O,A1,将C1绕点A1旋转180°得C2,交x轴于点A2;将C2绕点A2旋转180°得C3,交x轴于点A3;…如此进行下去,直至得C672.若P(2015,m)在图象上,则m=-2.
一段抛物线y=-x(x-3),(0≤x>3),记为C1,它与x轴交于点O,A1,将C1绕点A1旋转180°得C2,交x轴于点A2;将C2绕点A2旋转180°得C3,交x轴于点A3;…如此进行下去,直至得C672.若P(2015,m)在图象上,则m=-2.