题目内容
8.下列图案均是用长度相同的小木棒按一定的规律拼搭而成的:拼搭第1个图案需4根小木棒,拼搭第2个图案需16根小木棒,…,依此规律拼成第7个图案需小木棒( )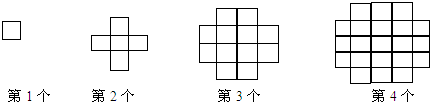
| A. | 76根 | B. | 104根 | C. | 136根 | D. | 144根 |
分析 由图形可知:拼搭第1个图案需2×(1+1)=4根小木棒,拼搭第2个图案需2×(1×2+3×2)=16根小木棒,拼搭第3个图案需2×(2×2+4×3)=32根小木棒,拼搭第4个图案需2×(3×2+5×4)=52根小木棒,…,依此规律得出拼成第n个图案需小木棒2[2(n-1)+n(n+1)]=2n2+6n-4根,由此代入求得答案.
解答 解:∵拼搭第1个图案需2×(1+1)=4根小木棒,
拼搭第2个图案需2×(1×2+3×2)=16根小木棒,
拼搭第3个图案需2×(2×2+4×3)=32根小木棒,
拼搭第4个图案需2×(3×2+5×4)=52根小木棒,
…
∴拼成第n个图案需小木棒2[2(n-1)+n(n+1)]=2n2+6n-4根,
则拼成第7个图案需小木棒2×49+42-4=136根.
故选:C.
点评 此题考查图形的变化规律,根据图形,纵横两个方向数出小棒,从简单入手,找出运算规律解决问题.

练习册系列答案
相关题目
18.一个不透明的盒子中装6个小球(除了颜色外无其他差别),从中随机抽取一个小球,共有3种可能的情况:红球、黄球和绿球,则随机摸出一球是红球的概率为( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | 无法确定 |
16.用加减法解方程组$\left\{\begin{array}{l}{11x+3z=9}\\{3x+2y+z=8}\\{2x-6y+4z=5}\end{array}\right.$,较方便的是( )
| A. | 先消去x,再解$\left\{\begin{array}{l}{22y+2z=61}\\{66y-38z=-33}\end{array}\right.$ | |
| B. | 先消去y,再解$\left\{\begin{array}{l}{11x+7z=29}\\{11x+3z=9}\end{array}\right.$ | |
| C. | 先消去z,再解$\left\{\begin{array}{l}{11x+3z=9}\\{11x+14y=27}\end{array}\right.$ | |
| D. | 先消去z,再解$\left\{\begin{array}{l}{2x-6y=-15}\\{19x+9y=8}\end{array}\right.$ |
