题目内容
8.已知关于x的方程x2-8x+m+1=0.(1)若$4-\sqrt{5}$是方程的一个根,求m的值及另一个根;
(2)若方程有两个不相等的实数根,求m的取值范围.
分析 (1)设另一个根为x2,由根与系数的关系得出$4-\sqrt{5}$+x2=8,($4-\sqrt{5}$)x2=m+1,即可求出m的值及另一个根;
(2)由判别式的意义得出△=b2-4ac=(-8)2-4×1×(m+1)>0,解不等式即可求解.
解答 解:(1)设另一个根为x2,由根与系数的关系可知
$4-\sqrt{5}$+x2=8,($4-\sqrt{5}$)x2=m+1,
解得x2=4+$\sqrt{5}$,m=10;
(2)若方程有两个不相等的实数根,则
△=(-8)2-4×1×(m+1)>0,
解得m<15.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0,a,b,c为常数)的根的判别式△=b2-4ac.当△>0时,方程有两个不相等的实数根;当△=0时,方程有两个相等的实数根;当△<0时,方程没有实数根.也考查了根与系数的关系.

练习册系列答案
相关题目
19.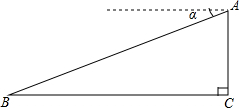 在寻找马航MH730航班的过程中,某搜寻飞机在空中A处发现海面上一块疑似漂浮目标B,从飞机上看目标B的俯角为α,此时飞机的飞行高度AC=1200米,tanα=$\frac{5}{12}$,则飞机距离疑似目标B的距离AB为( )
在寻找马航MH730航班的过程中,某搜寻飞机在空中A处发现海面上一块疑似漂浮目标B,从飞机上看目标B的俯角为α,此时飞机的飞行高度AC=1200米,tanα=$\frac{5}{12}$,则飞机距离疑似目标B的距离AB为( )
 在寻找马航MH730航班的过程中,某搜寻飞机在空中A处发现海面上一块疑似漂浮目标B,从飞机上看目标B的俯角为α,此时飞机的飞行高度AC=1200米,tanα=$\frac{5}{12}$,则飞机距离疑似目标B的距离AB为( )
在寻找马航MH730航班的过程中,某搜寻飞机在空中A处发现海面上一块疑似漂浮目标B,从飞机上看目标B的俯角为α,此时飞机的飞行高度AC=1200米,tanα=$\frac{5}{12}$,则飞机距离疑似目标B的距离AB为( )| A. | 3120米 | B. | 2800$\sqrt{3}$米 | C. | 3260米 | D. | 3000$\sqrt{3}$米 |
3.若(a+b)(a+b+2)=8,则a+b的值为( )
| A. | -4 | B. | 2 | C. | 4 | D. | -4或2 |
13.下列实数中,属无理数的是( )
| A. | 3.1415926 | B. | $\frac{22}{7}$ | C. | $\sqrt{2}$ | D. | (π-1)0 |
20.数轴上A、B两点表示的数分别为-1和$\sqrt{2}$,数轴上点C在点A的左侧,到A点的距离等于点B到点A的距离,则点C所表示的数为( )
| A. | $-2+\sqrt{2}$ | B. | $-1+\sqrt{2}$ | C. | $3-\sqrt{2}$ | D. | $-2-\sqrt{2}$ |
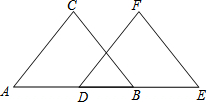 已知:如图,BC∥EF,AD=BE,BC=EF
已知:如图,BC∥EF,AD=BE,BC=EF