题目内容
19.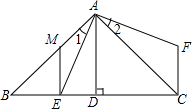 如图,△ABC中,∠BAC=90°,AB=AC,AD⊥BC,垂足是D,AE平分∠BAD,交BC于点E.在△ABC外取一点F,使FA⊥AE,FC⊥BC.
如图,△ABC中,∠BAC=90°,AB=AC,AD⊥BC,垂足是D,AE平分∠BAD,交BC于点E.在△ABC外取一点F,使FA⊥AE,FC⊥BC.(1)求证:BE=CF;
(2)在AB上取一点M,使BM=2DE,连接ME.试判断ME与BC是否垂直,并说明理由.
分析 (1)首先根据∠BAC=90°,AF⊥AE可得∠1=∠2,然后根据FC⊥BC,得出∠B=∠FCA=45°,根据条件利用ASA证明△ABE≌△ACF,继而可得BE=CF;
(2)过点E作EH⊥AB于H,求出△BEH是等腰直角三角形,然后求出HE=BH,再根据角平分线上的点到角的两边距离相等可得DE=HE,然后求出HE=HM,从而得到△HEM是等腰直角三角形,再根据等腰直角三角形的性质求解即可.
解答 解:(1)∵∠BAC=90°,AF⊥AE,
∴∠1+∠EAC=90°,∠2+∠EAC=90°
∴∠1=∠2,
又∵AB=AC,
∴∠B=∠ACB=45°,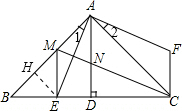
∵FC⊥BC,
∴∠FCA=90°-∠ACB=90°-45°=45°,
∴∠B=∠FCA,
在△ABE和△ACF中,
$\left\{\begin{array}{l}{∠B=∠FCA}\\{∠1=∠2}\\{AB=AC}\end{array}\right.$,
∴△ABE≌△ACF(ASA),
∴BE=CF;
(2)如图,过点E作EH⊥AB于H,则△BEH是等腰直角三角形,
∴HE=BH,∠BEH=45°,
∵AE平分∠BAD,AD⊥BC,
∴DE=HE,
∴DE=BH=HE,
∵BM=2DE,
∴HE=HM,
∴△HEM是等腰直角三角形,
∴∠MEH=45°,
∴∠BEM=45°+45°=90°,
∴ME⊥BC.
点评 本题考查了全等三角形的判定与性质,等腰直角三角形的判定与性质,角平分线上的点到角的两边距离相等的性质,熟记性质并作辅助线构造出等腰直角三角形和全等三角形是解题的关键.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案
相关题目
14.下列说法中,错误的是( )
| A. | 三角形中至少有一个内角不小于60° | |
| B. | 三角形的角平分线、中线、高均在三角形的内部 | |
| C. | 有一个角是60°的等腰三角形是等边三角形 | |
| D. | 多边形的外角和等于360° |
11.一个数的绝对值小于3,那么这个数不可能是( )
| A. | 0 | B. | 2 | C. | -2 | D. | -3 |
8.下列命题错误的是( )
| A. | 有一个角是60°的等腰三角形是等边三角形 | |
| B. | 有两个角等于60°的三角形是等边三角形 | |
| C. | 三个角都相等的三角形是等边三角形 | |
| D. | 两个角相等的等腰三角形是等边三角形 |
9.下列说法正确的是( )
| A. | 线段AB和线段BA表示的不是同一条线段 | |
| B. | 射线AB和射线BA表示的是同一条射线 | |
| C. | 若点P是线段AB的中点,则PA=$\frac{1}{2}$AB | |
| D. | 线段AB叫做A、B两点间的距离 |
 如图,a,b为数轴上的两点表示的有理数,在a+b,a-b,b-a,ab,|a-b|,|b|-|a|中负数的个数有( )
如图,a,b为数轴上的两点表示的有理数,在a+b,a-b,b-a,ab,|a-b|,|b|-|a|中负数的个数有( )