题目内容
4.解下列分式方程:(1)$\frac{2x-5}{x-2}$=$\frac{3}{2-x}$
(2)$\frac{12}{{x}^{2}-9}$-$\frac{2}{x-3}$=$\frac{1}{x+3}$.
分析 两分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答 解:(1)去分母得:2x-5=-3,
解得:x=1,
经检验x=1是分式方程的解;
(2)去分母得:12-2(x+3)=x-3,
去括号得:12-2x-6=x-3,
移项合并得:-3x=-9,
解得:x=3,
经检验x=3是增根,分式方程无解.
点评 此题考查了解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.下列各组图形中不是位似图形的是( )
| A. |  | B. |  | C. |  | D. |  |
12. 如图是两个全等三角形,图中的字母表示三角形的边长,则∠1的度数是( )
如图是两个全等三角形,图中的字母表示三角形的边长,则∠1的度数是( )
 如图是两个全等三角形,图中的字母表示三角形的边长,则∠1的度数是( )
如图是两个全等三角形,图中的字母表示三角形的边长,则∠1的度数是( )| A. | 54° | B. | 60° | C. | 66° | D. | 76° |
14.点(0,3)的位置在( )
| A. | x轴正半轴 | B. | x轴负半轴 | C. | y轴正半轴 | D. | y轴负半轴 |
 如图是一张月历表,在此月历表上可以用一个矩形任意圈出2×2个位置上相邻的数(如2,3,9,10).如果圈出的4个数中最大数与最小数的积为128,则这4个数中最小的数是8.
如图是一张月历表,在此月历表上可以用一个矩形任意圈出2×2个位置上相邻的数(如2,3,9,10).如果圈出的4个数中最大数与最小数的积为128,则这4个数中最小的数是8.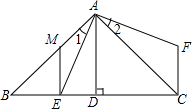 如图,△ABC中,∠BAC=90°,AB=AC,AD⊥BC,垂足是D,AE平分∠BAD,交BC于点E.在△ABC外取一点F,使FA⊥AE,FC⊥BC.
如图,△ABC中,∠BAC=90°,AB=AC,AD⊥BC,垂足是D,AE平分∠BAD,交BC于点E.在△ABC外取一点F,使FA⊥AE,FC⊥BC.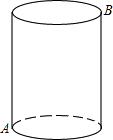 如图所示,一个圆柱体的高为6cm,底面半径为$\frac{8}{π}$cm,在圆柱体下底面A点有一只蚂蚁,想吃到上底面B点的一粒砂糖(A、B是圆柱体上、下底面相对的两点),则这只蚂蚁从A出点沿着圆柱表面爬到B点的最短路线的长是10cm.
如图所示,一个圆柱体的高为6cm,底面半径为$\frac{8}{π}$cm,在圆柱体下底面A点有一只蚂蚁,想吃到上底面B点的一粒砂糖(A、B是圆柱体上、下底面相对的两点),则这只蚂蚁从A出点沿着圆柱表面爬到B点的最短路线的长是10cm. 如图,在△ABC中,AB=AD=DC,∠BAD=24°,求∠BAC的度数.
如图,在△ABC中,AB=AD=DC,∠BAD=24°,求∠BAC的度数.