题目内容
10.解不等式组$\left\{\begin{array}{l}{\frac{1}{2}x-2≤0}\\{5-3(x-1)<4+x}\end{array}\right.$,并把解集在数轴上表示出来.分析 先求出两个不等式的解集,再求其公共解.
解答 解:$\left\{\begin{array}{l}{\frac{1}{2}x-2≤0①}\\{5-3(x-1)<4+x②}\end{array}\right.$,
由①得,x≤4,
由②得,x>1,
所以,原不等式组的解集是1<x≤4.
在数轴上表示如下:
点评 本题考查了一元一次不等式组的解法,在数轴上表示不等式组的解集,需要把每个不等式的解集在数轴上表示出来(>,≥向右画;<,≤向左画),在表示解集时“≥”,“≤”要用实心圆点表示;“<”,“>”要用空心圆点表示.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
5.1500万(即15000000)这个数用科学记数法可表示为( )
| A. | 1.5×105 | B. | 1.5×106 | C. | 1.5×107 | D. | 1.8×108 |
15.下列各组图形中不是位似图形的是( )
| A. |  | B. |  | C. |  | D. |  |
2. 我县教育局为提高教师的教学水平,在全范围举行了数学比武,其中10名参加决赛的教师的参赛成绩统计如图所示,对于这10名教师的参赛成绩,下列说法中错误的是( )
我县教育局为提高教师的教学水平,在全范围举行了数学比武,其中10名参加决赛的教师的参赛成绩统计如图所示,对于这10名教师的参赛成绩,下列说法中错误的是( )
 我县教育局为提高教师的教学水平,在全范围举行了数学比武,其中10名参加决赛的教师的参赛成绩统计如图所示,对于这10名教师的参赛成绩,下列说法中错误的是( )
我县教育局为提高教师的教学水平,在全范围举行了数学比武,其中10名参加决赛的教师的参赛成绩统计如图所示,对于这10名教师的参赛成绩,下列说法中错误的是( )| A. | 众数是90 | B. | 中位数是90 | C. | 平均数是90 | D. | 极差是15 |
20.用一个平面截正方体所得的截面图形不可能是( )
| A. | 六边形 | B. | 五边形 | C. | 菱形 | D. | 直角三角形 |
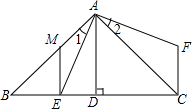 如图,△ABC中,∠BAC=90°,AB=AC,AD⊥BC,垂足是D,AE平分∠BAD,交BC于点E.在△ABC外取一点F,使FA⊥AE,FC⊥BC.
如图,△ABC中,∠BAC=90°,AB=AC,AD⊥BC,垂足是D,AE平分∠BAD,交BC于点E.在△ABC外取一点F,使FA⊥AE,FC⊥BC.