题目内容
6.化简$\frac{a^2}{a-b}+\frac{b^2}{b-a}$的结果是( )| A. | a+b | B. | b-a | C. | a-b | D. | -a-b |
分析 原式变形后,利用同分母分式的减法法则计算即可得到结果.
解答 解:原式=$\frac{{a}^{2}}{a-b}$-$\frac{{b}^{2}}{a-b}$=$\frac{{a}^{2}-{b}^{2}}{a-b}$=$\frac{(a+b)(a-b)}{a-b}$=a+b,
故选A
点评 此题考查了分式的加减法,分式加减法的关键是通分,通分的关键是找出各分母的最简公分母.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
17.已知a,b为两个连续整数,且a<$\sqrt{19}$-1<b,则这两个整数是( )
| A. | 1和2 | B. | 2和3 | C. | 3和4 | D. | 4和5 |
14.下列图案中,可以看做是中心对称图形的有( )
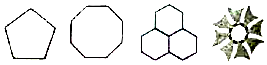

| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
1.若分式$\frac{x+2}{x-1}$有意义,则x的取值范围是( )
| A. | x≥1 | B. | x≠1 | C. | x≥-2 | D. | x≠-2 |
11.实数6的算术平方根是( )
| A. | 36 | B. | 6 | C. | $\sqrt{6}$ | D. | ±$\sqrt{6}$ |
18.下列根式中不是最简二次根式的是( )
| A. | $\sqrt{10}$ | B. | $\sqrt{12}$ | C. | $\sqrt{14}$ | D. | $\frac{\sqrt{17}}{2}$ |