题目内容
14.△ABC的三边长分别为$\sqrt{2}$,$\sqrt{10}$和2,△A′B′C′的两边长分别为1和$\sqrt{5}$.如果△ABC∽△A′B′C′,则△A′B′C′第三边的长为( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\sqrt{2}$ | C. | 2 | D. | 2$\sqrt{2}$ |
分析 设△A′B′C′第三边的长为x,根据相似三角形的性质得出比例式,即可求出x.
解答 解:设△A′B′C′第三边的长为x,
∵△ABC∽△A′B′C′,△ABC的三边长分别为$\sqrt{2}$,$\sqrt{10}$和2,△A′B′C′的两边长分别为1和$\sqrt{5}$,
∴$\frac{\sqrt{2}}{1}$=$\frac{\sqrt{10}}{\sqrt{5}}$=$\frac{2}{x}$,
解得:x=$\sqrt{2}$,
故选B.
点评 本题考查了相似三角形的性质的应用,能得出比例式是解此题的关键,注意:相似三角形的对应边的比相等.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
19.将一元二次方程2(x+2)2+(x+3)(x-2)=-11化为一般形式为( )
| A. | x2+3x+4=0 | B. | 3x2+9x+12=0 | C. | 3x2+8x+13=0 | D. | 3x2+9x+13=0 |
 如图,矩形纸片ABCD的长为6$\sqrt{3}$cm,宽为6cm,将其沿对角线折叠,则其重叠部分的面积等于12$\sqrt{3}$cm2.
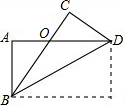
如图,矩形纸片ABCD的长为6$\sqrt{3}$cm,宽为6cm,将其沿对角线折叠,则其重叠部分的面积等于12$\sqrt{3}$cm2. 如图,已知AB∥CD,OA=2,AD=9,OB=5,DC=12,∠A=58°,∠AOB=72°,求AB,OC的长及∠C的度数.
如图,已知AB∥CD,OA=2,AD=9,OB=5,DC=12,∠A=58°,∠AOB=72°,求AB,OC的长及∠C的度数.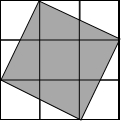 如图,在3×3的方格中,有一阴影正方形,设每一个小方格的边长为1个单位.请解决下面的问题.
如图,在3×3的方格中,有一阴影正方形,设每一个小方格的边长为1个单位.请解决下面的问题.