题目内容
13.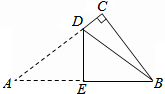 如图,已知Rt△ABC中,∠C=90°,AB=10cm,BC=6cm.现将△ABC沿折痕DE进行折叠,使顶点A,B重合,则△DCB的周长等于14cm.
如图,已知Rt△ABC中,∠C=90°,AB=10cm,BC=6cm.现将△ABC沿折痕DE进行折叠,使顶点A,B重合,则△DCB的周长等于14cm.
分析 在Rt△ABC中,根据勾股定理得到AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=8cm,由折叠的性质得到AD=BD,于是得到结论.
解答 解:在Rt△ABC中,∠C=90°,AB=10cm,BC=6cm,
∴AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=8cm,
∵将△ABC沿折痕DE进行折叠,使顶点A,B重合,
∴AD=BD,
∴△DCB的周长=BD+CD+BC=AD+CD+BC=AC+BC=14cm,
故答案为:14.
点评 本题主要考查了翻折变换、勾股定理,求三角形的周长,牢固掌握翻折变换的性质是灵活解题的基础和关键.

练习册系列答案
相关题目
8. 如图所示,已知AB=DB,∠ABD=∠CBE,添加下列哪一个条件后,仍不能证明△ABC≌△DBE的是( )
如图所示,已知AB=DB,∠ABD=∠CBE,添加下列哪一个条件后,仍不能证明△ABC≌△DBE的是( )
 如图所示,已知AB=DB,∠ABD=∠CBE,添加下列哪一个条件后,仍不能证明△ABC≌△DBE的是( )
如图所示,已知AB=DB,∠ABD=∠CBE,添加下列哪一个条件后,仍不能证明△ABC≌△DBE的是( )| A. | DE=AC | B. | ∠BDE=∠BAC | C. | ∠DEB=∠ACB | D. | BE=BC |
 如图,已知∠DAC=∠B,请你分析∠ADC与∠BAC之间的大小关系.
如图,已知∠DAC=∠B,请你分析∠ADC与∠BAC之间的大小关系.
 如图,已知∠BOD=80°,四边形ABCD的四个顶点都在圆O上,那么∠DAB的度数为140°.
如图,已知∠BOD=80°,四边形ABCD的四个顶点都在圆O上,那么∠DAB的度数为140°.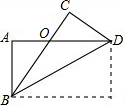 如图,矩形纸片ABCD的长为6$\sqrt{3}$cm,宽为6cm,将其沿对角线折叠,则其重叠部分的面积等于12$\sqrt{3}$cm2.
如图,矩形纸片ABCD的长为6$\sqrt{3}$cm,宽为6cm,将其沿对角线折叠,则其重叠部分的面积等于12$\sqrt{3}$cm2.