题目内容
5. 如图,矩形ABCD中,AB=3,BC=4,点E是线段CB上的异于B、C的动点,AF⊥AE交线段CD的延长线于点F,EF与AD交于点M.
如图,矩形ABCD中,AB=3,BC=4,点E是线段CB上的异于B、C的动点,AF⊥AE交线段CD的延长线于点F,EF与AD交于点M.(1)求证:△ABE∽△ADF;
(2)若AE⊥BD,求BE长;
(3)若△AEM是以AE为腰的等腰三角形,求BE的长.
分析 (1)由矩形的性质得出∠BAD=∠ABC=∠C=∠ADC=∠ADF=90°,AD∥BC,证出∠BAE=∠DAF,即可得出结论;
(2)证明△ABE∽△DAB,得出对应边成比例,即可得出答案;
(3)①当AE=AM时,证明△AEF≌△CEF(AAS),得出AE=CE,设BE=x,则AE=CE=4-x,Rt△ABE中,由勾股定理得出方程,解方程即可;
②当AE=EM时,过点E作EN⊥AD于点N,则AN=MN=BE=x,EN∥DF,由(1)得:△ABE∽△ADF,得出对应边成比例求出DF=$\frac{4}{3}$x,由平行线证明△EMN∽△FMD,得出对应边成比例,得出方程,解方程即可.
解答 (1)证明:∵四边形ABCD是矩形,
∴∠BAD=∠ABC=∠C=∠ADC=∠ADF=90°,AD∥BC,
∵AF⊥AE,∴∠EAF=90°,
∴∠BAD=∠EAF,
∴∠BAE=∠DAF,
∵∠ABE=∠ADF=90°,
∴△ABE∽△ADF.
(2)解:∵AD∥BC,
∴∠AEB=∠DAE,
∵AE⊥BD,
∴∠BAE+∠ABD=90°,
∵∠BAE+∠AEB=90°,
∴∠ABD=∠AEB,
∴∠AEB=∠ABD,
又∵∠ABE=∠BAD=90°,
∴△ABE∽△DAB,
∴$\frac{AB}{DA}=\frac{BE}{AB}$,即$\frac{3}{4}=\frac{BE}{3}$,
解得:BE=$\frac{9}{4}$;
(3)解:分两种情况:
①当AE=AM时,∠AEF=∠AME,
∵AF⊥AE,
∴∠EAF=90°,
∵AD∥BC,
∴∠AME=∠CEF,
∴∠AEF=∠CEF,
在△AEF和△CEF中,$\left\{\begin{array}{l}{∠AEF=∠CEF}&{\;}\\{∠EAF=∠C=90°}&{\;}\\{EF=EF}&{\;}\end{array}\right.$,
∴△AEF≌△CEF(AAS),
∴AE=CE,
设BE=x,则AE=CE=4-x,Rt△ABE中,
由勾股定理得:x2+32=(4-x)2,解得:x=$\frac{7}{8}$;
②当AE=EM时,过点E作EN⊥AD于点N,如图所示:
则AN=MN=BE=x,EN∥DF,
由(1)得:△ABE∽△ADF,
∴$\frac{AB}{AD}=\frac{BE}{DF}$,即$\frac{3}{4}=\frac{x}{DF}$,
解得:DF=$\frac{4}{3}$x,
∵EN∥DF,
∴∴△EMN∽△FMD,
∴$\frac{EN}{DF}=\frac{MN}{DM}$,即$\frac{3}{\frac{4}{3}x}=\frac{x}{4-2x}$,
解得:x=$\frac{3}{2}$或x=-6(舍去),
∴BE=$\frac{3}{2}$;
综上所述,若△AEM是以AE为腰的等腰三角形,BE长为$\frac{7}{8}$或$\frac{3}{2}$.
点评 本题是四边形综合题目,考查了矩形的性质、全等三角形的判定与性质、相似三角形的判定与性质、等腰三角形的性质、勾股定理等知识;本题综合性强,有一定难度,熟练掌握矩形的性质和等腰三角形的性质,证明三角形全等和三角形相似是解决问题的关键.

 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案①不带根号的数都是有理数;②无限小数都是无理数;
③任何实数都可以进行开立方运算;④$\frac{\sqrt{3}}{5}$不是分数.
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
| A. | (a-3)2=a2-9 | B. | a2•a4=a8 | C. | $\sqrt{9}$=±3 | D. | x6÷x3=x3 |
| A. | 8 | B. | 9 | C. | 10 | D. | 11 |

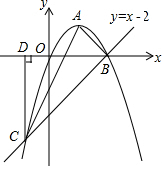 如图,已知抛物线y=-x2+2x的顶点为A,直线y=x-2与抛物线交于B,C两点.
如图,已知抛物线y=-x2+2x的顶点为A,直线y=x-2与抛物线交于B,C两点. 如图,在平面直角坐标系中,有若干个横纵坐标分别为整数的点,其顺序按图中“→”方向排序,如(1,0)→(2,0)→(2,1)→(1,1)→(1,2)→(2,2)…根据这个规律,则第2018个点的横坐标为( )
如图,在平面直角坐标系中,有若干个横纵坐标分别为整数的点,其顺序按图中“→”方向排序,如(1,0)→(2,0)→(2,1)→(1,1)→(1,2)→(2,2)…根据这个规律,则第2018个点的横坐标为( )