题目内容
 如图,在扇形OAB中,∠AOB=105°,半径OA=10,将扇形OAB沿过点B的直线折叠,点O恰好落在弧AB上的点D处,折痕BC交OA于点C,则图中阴影部分面积为
如图,在扇形OAB中,∠AOB=105°,半径OA=10,将扇形OAB沿过点B的直线折叠,点O恰好落在弧AB上的点D处,折痕BC交OA于点C,则图中阴影部分面积为考点:扇形面积的计算,翻折变换(折叠问题)
专题:
分析:先连接OD,由折叠的性质,可得CD=CO,BD=BO,∠DBC=∠OBC,则可得△OBD是等边三角形,△OCD是等腰直角三角形,故可得出OC的长,再根据S阴影=S扇形AOB-S△OCD-S△OBD即可得出结论.
解答: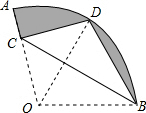 解:连接OD,
解:连接OD,
∵△CBD由△CBO翻折而成,
∴CD=CO,BD=BO,∠DBC=∠OBC,
∴△OBD是等边三角形.
∵∠AOB=105°,
∴∠COD=∠CDO=45°,
∴△OCD是等腰直角三角形.
∵半径OA=10,
∴OC=
=
=5
,
∴S阴影=S扇形AOB-S△OCD-S△OBD=
-
×5
×5
-
×10×10×
=
-25-25
.
故答案为:
-25-25
.
 解:连接OD,
解:连接OD,∵△CBD由△CBO翻折而成,
∴CD=CO,BD=BO,∠DBC=∠OBC,
∴△OBD是等边三角形.
∵∠AOB=105°,
∴∠COD=∠CDO=45°,
∴△OCD是等腰直角三角形.
∵半径OA=10,
∴OC=
|
|
| 2 |
∴S阴影=S扇形AOB-S△OCD-S△OBD=
| 105π×102 |
| 360 |
| 1 |
| 2 |
| 2 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 75π |
| 6 |
| 3 |
故答案为:
| 75π |
| 6 |
| 3 |
点评:此题考查的是扇形面积公式,在解答此题时要注意数形结合思想的应用,注意辅助线的作法.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
二次函数y=-3x2+12的图象与坐标轴的交点个数为( )
| A、1个 | B、2个 | C、3个 | D、4个 |
 若有理数a,b,c在数轴上的位置如图所示,在下列结论中:①a-b>0②ab<0③a+b<0④b(a-c)>0,其中正确的个数有( )
若有理数a,b,c在数轴上的位置如图所示,在下列结论中:①a-b>0②ab<0③a+b<0④b(a-c)>0,其中正确的个数有( )| A、1个 | B、2个 | C、3个 | D、4个 |
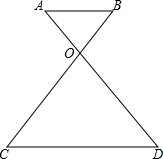 如图,AD与BC交与点O,且AB∥CD.
如图,AD与BC交与点O,且AB∥CD.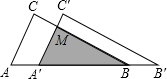 如图所示,把△ABC沿AB边平移到△A′B′C′的位置,它们的重叠部分(即图中的阴影部分)的面积是△ABC的面积的一半,若AB=
如图所示,把△ABC沿AB边平移到△A′B′C′的位置,它们的重叠部分(即图中的阴影部分)的面积是△ABC的面积的一半,若AB=