题目内容
3.已知点A(-2,y1),B(3,y2)是反比例函数y=$\frac{k}{x}$(k<0)图象上的两点,则有( )| A. | y1<0<y2 | B. | y2<0<y1 | C. | y1<y2<0 | D. | y2<y1<0 |
分析 先根据函数解析式中的比例系数k确定函数图象所在的象限,再根据各象限内点的坐标特点解答.
解答 解:∵反比例函数y=$\frac{k}{x}$(k<0)中,k<0,
∴此函数图象在二、四象限,
∵-2<0,
∴点A(-2,y1)在第二象限,
∴y1>0,
∵3>0,
∴B(3,y2)点在第四象限,
∴y2<0,
∴y1,y2的大小关系为y2<0<y1.
故选B.
点评 此题考查的是反比例函数图象上点的坐标特点及平面直角坐标系中各象限内点的坐标特点,比较简单.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案
相关题目
14.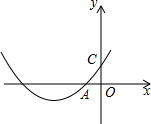 二次函数y=ax2+bx+c的图象如图,点C在y轴的正半轴上,且OA=OC,则( )
二次函数y=ax2+bx+c的图象如图,点C在y轴的正半轴上,且OA=OC,则( )
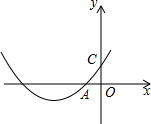 二次函数y=ax2+bx+c的图象如图,点C在y轴的正半轴上,且OA=OC,则( )
二次函数y=ax2+bx+c的图象如图,点C在y轴的正半轴上,且OA=OC,则( )| A. | ac+1=b | B. | ab+1=c | C. | bc+1=a | D. | 以上都不是 |
18. 如图,将矩形纸片ABCD折叠,使点A与点C重合,折痕为EF,若AB=4,BC=2,那么线段EF的长为( )
如图,将矩形纸片ABCD折叠,使点A与点C重合,折痕为EF,若AB=4,BC=2,那么线段EF的长为( )
 如图,将矩形纸片ABCD折叠,使点A与点C重合,折痕为EF,若AB=4,BC=2,那么线段EF的长为( )
如图,将矩形纸片ABCD折叠,使点A与点C重合,折痕为EF,若AB=4,BC=2,那么线段EF的长为( )| A. | 2$\sqrt{5}$ | B. | $\sqrt{5}$ | C. | $\frac{4\sqrt{5}}{5}$ | D. | $\frac{2\sqrt{5}}{5}$ |
13.若关于x的方程x2+x-a+$\frac{9}{4}$=0有两个不相等的实数根,则实数a的取值范围是( )
| A. | a≥2 | B. | a≤2 | C. | a>2 | D. | a<2 |
 如图,关于x的二次函数y=x2+bx+c的图象与x轴交于点A(1,0)和点B,与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.
如图,关于x的二次函数y=x2+bx+c的图象与x轴交于点A(1,0)和点B,与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.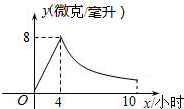 某药品研究所开发一种抗菌新药,经多年动物实验,首次用于临床人体试验,测得成人服药后血液中药物浓度y(微克/毫升)与服药时间x小时之间函数关系如图所示(当4≤x≤10时,y与x成反比例).
某药品研究所开发一种抗菌新药,经多年动物实验,首次用于临床人体试验,测得成人服药后血液中药物浓度y(微克/毫升)与服药时间x小时之间函数关系如图所示(当4≤x≤10时,y与x成反比例).


