题目内容
10.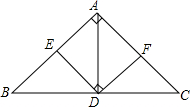 如图,在三角形ABC中,∠BAC=90°,AB=AC,AD是斜边BC上的高,点E为AB边上一点,连接ED,过点D作DF⊥DE交AC于点F.求证:△BDE≌△ADF.
如图,在三角形ABC中,∠BAC=90°,AB=AC,AD是斜边BC上的高,点E为AB边上一点,连接ED,过点D作DF⊥DE交AC于点F.求证:△BDE≌△ADF.
分析 根据等腰直角三角形的性质和全等三角形的判定定理ASA证得结论.
解答 证明:∵在三角形ABC中,∠BAC=90°,AB=AC,AD是斜边BC上的高,
∴∠B=∠C=45°,AD是BC边上的中垂线,
∴∠B=∠FAD=45°,BD=AD.
又DF⊥DE,
∴∠BDE=∠ADF,
∴在△BDE与△ADF中,$\left\{\begin{array}{l}{∠B=∠FAD}\\{BD=AD}\\{∠BDE=∠ADF}\end{array}\right.$,
∴△BDE≌△ADF(ASA).
点评 本题考查了全等三角形的判定.全等三角形的5种判定方法中,选用哪一种方法,取决于题目中的已知条件,若已知两边对应相等,则找它们的夹角或第三边;若已知两角对应相等,则必须再找一组对边对应相等,且要是两角的夹边,若已知一边一角,则找另一组角,或找这个角的另一组对应邻边.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
2.已知a,b,c是△ABC三边的长,b>a=c,且方程ax2-$\sqrt{2}$bx+c=0的两根的差的绝对值等于$\sqrt{2}$,则△ABC中最大角的度数是( )
| A. | 150° | B. | 120° | C. | 90° | D. | 60° |
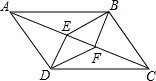 如图,?ABCD中,DE⊥AC,BF⊥AC,垂足分别为E、F,求证:BE∥DF.
如图,?ABCD中,DE⊥AC,BF⊥AC,垂足分别为E、F,求证:BE∥DF.