题目内容
8.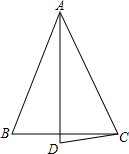 如图,在△ABC中,∠B=∠C,点D在△ABC外,∠ADC=∠ACD.
如图,在△ABC中,∠B=∠C,点D在△ABC外,∠ADC=∠ACD.(1)如果∠BAC=50°,∠DAC=30°,求∠BCD的度数;
(2)若∠BAD=20°,求∠BCD度数;
(3)若∠BAD=N°,求∠BCD的度数.
分析 (1)根据等腰三角形的判定和三角形的内角和得到∠B=∠ACB=65°,∠ADC=∠ACD=75°,根据角的和差即可得到结论;
(2)根据等腰三角形的判定定理得到AB=AC=AD,推出B,D,C三点在以A为圆心,以AB为半径的圆上,根据圆周角定理即可得到结论;
(3)根据等腰三角形的判定定理得到AB=AC=AD,推出B,D,C三点在以A为圆心,以AB为半径的圆上,根据圆周角定理即可得到结论.
解答 解:(1)∵∠BAC=50°,∠DAC=30°,
∴∠B=∠ACB=65°,∠ADC=∠ACD=75°,
∴∠BCD=∠ACD-∠ACB=10°;
(2)∵∠B=∠C,∠ADC=∠ACD,
∴AB=AC=AD,
∴B,D,C三点在以A为圆心,以AB为半径的圆上,
∴∠BCD=$\frac{1}{2}∠$BAD=10°,;
(3)∵∠B=∠C,∠ADC=∠ACD,
∴AB=AC=AD,
∴B,D,C三点在以A为圆心,以AB为半径的圆上,
∴∠BCD=$\frac{1}{2}∠$BAD=$\frac{N°}{2}$.
点评 本题考查了线段垂直平分线的性质,等腰三角形的判定和性质,熟练掌握各性质定理是解题的关键.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
 画图并填空:
画图并填空: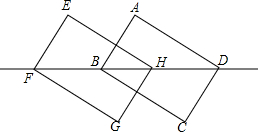 如图,在长方形ABCD中,AB=CD=6,AD=BC=8,对角线BD=10,现将长方形沿对角线BD所在直线向左平移4个单位得到长方形EFGH,则点F到直线AD的距离是( )
如图,在长方形ABCD中,AB=CD=6,AD=BC=8,对角线BD=10,现将长方形沿对角线BD所在直线向左平移4个单位得到长方形EFGH,则点F到直线AD的距离是( )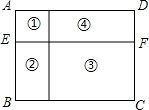 如图,要用60m的篱笆在一块足够大的空地上围出四个花园,已知①号花园为正方形,且④号花园的周长等于①号和②号花园周长之和.设CD的长为xm,②号花园的面积为ym2.
如图,要用60m的篱笆在一块足够大的空地上围出四个花园,已知①号花园为正方形,且④号花园的周长等于①号和②号花园周长之和.设CD的长为xm,②号花园的面积为ym2. 如图,双曲线y=$\frac{k}{x}$(k>0)与直线y=-$\frac{1}{2}$x+4相交于A,B两点.
如图,双曲线y=$\frac{k}{x}$(k>0)与直线y=-$\frac{1}{2}$x+4相交于A,B两点.