题目内容
9.已知一条线段c的长为3,现有四张正面分别有数字4,5,$\sqrt{7},\sqrt{2}$的不透明卡片,它们除了数字不同外其余全部相同,现将它们背面朝上,洗匀后从中任取一张,将该卡片上的数记为a,将卡片放回后再从中任取一张,将卡片上的数字记为b,则以a,b,c为三边能够成直角三角形的概率为$\frac{3}{8}$.分析 首先根据题意画出树状图,然后由树状图求得所有等可能的结果与以a,b,c为三边能够成直角三角形的情况,再利用概率公式即可求得答案.
解答 解:画树状图得:
∵共有16种等可能的结果,以a,b,c为三边能够成直角三角形的6种情况,
∴以a,b,c为三边能够成直角三角形的概率为:$\frac{6}{16}$=$\frac{3}{8}$.
故答案为:$\frac{3}{8}$.
点评 此题考查了列表法或树状图法求概率.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
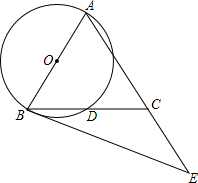 如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,点E在AC的延长线上,且∠CBE=$\frac{1}{2}$∠BAC.
如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,点E在AC的延长线上,且∠CBE=$\frac{1}{2}$∠BAC.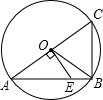 如图,AC是⊙O的直径,OE⊥AC交弦AB于E,若BC=4,S△AOE=5,则sin∠BOE的值为$\frac{3}{5}$.
如图,AC是⊙O的直径,OE⊥AC交弦AB于E,若BC=4,S△AOE=5,则sin∠BOE的值为$\frac{3}{5}$.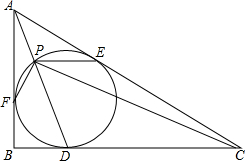 在直角三角形ABC中,∠B=90°,它的内切圆分别与边BC,CA,AB相切与点D,E,F,连接AD,与内切圆相交于另一点P,连接PC,PE,PF.已知PC⊥PF,求证:
在直角三角形ABC中,∠B=90°,它的内切圆分别与边BC,CA,AB相切与点D,E,F,连接AD,与内切圆相交于另一点P,连接PC,PE,PF.已知PC⊥PF,求证: