题目内容
16.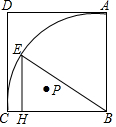 如图,正方形ABCD,以B为圆心,BC长为半径画弧,点E在圆弧上,EH⊥BC于点H,P是△EHB的内心,AB=2,则AP的最小值为$\sqrt{10}$-$\sqrt{2}$.
如图,正方形ABCD,以B为圆心,BC长为半径画弧,点E在圆弧上,EH⊥BC于点H,P是△EHB的内心,AB=2,则AP的最小值为$\sqrt{10}$-$\sqrt{2}$.
分析 首先证明点P的运动轨迹是圆弧,以BC为斜边在BC的下方作等腰直角三角形BCO,则以点O为圆心,OB为半径的⊙O是点P的轨迹,因为AP≤AO-OP,所以当O、P、A共线时,PA的值最小.
解答 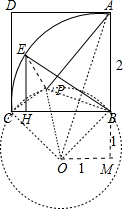 解:连接PE、PC、PB.
解:连接PE、PC、PB.
∵P是△EHB的内心,∠EHB=90°,
∴∠EPB=180°-$\frac{1}{2}$(∠HEB+∠HBE)=135°,
∵BC=BE,∠PBC=∠PBE,PB=PB,
∴△PBC≌△PBE,
∴∠BPC=∠BPE=135°(定角),
∴点P的运动轨迹是圆弧,以BC为斜边在BC的下方作等腰直角三角形BCO,连接OP、OA.
则以点O为圆心,OB为半径的⊙O是点P的轨迹,
∵AP≤AO-OP,
∴当O、P、A共线时,PA的值最小,
作OM⊥AB于M.易知OB=$\sqrt{2}$,OF=BF=1,OA=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$,
∴PA的最小值为$\sqrt{10}$-$\sqrt{2}$,
故答案为$\sqrt{10}$-$\sqrt{2}$.
点评 本题考查三角形的内切圆与内心、正方形的性质、三角形的三边关系等知识,解题的关键是正确寻找点P的运动轨迹,学会添加辅助圆解决问题,属于中考压轴题.

练习册系列答案
相关题目
12.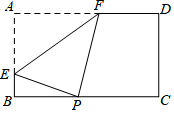 如图,矩形纸片ABCD中,AB=6,AD=10,P是边BC上的动点,现将纸片折叠,使点A与点P重合,折痕与矩形边的交点分别是E,F,要使折痕始终与边AB,AD有交点,则BP的取值范围是( )
如图,矩形纸片ABCD中,AB=6,AD=10,P是边BC上的动点,现将纸片折叠,使点A与点P重合,折痕与矩形边的交点分别是E,F,要使折痕始终与边AB,AD有交点,则BP的取值范围是( )
 如图,矩形纸片ABCD中,AB=6,AD=10,P是边BC上的动点,现将纸片折叠,使点A与点P重合,折痕与矩形边的交点分别是E,F,要使折痕始终与边AB,AD有交点,则BP的取值范围是( )
如图,矩形纸片ABCD中,AB=6,AD=10,P是边BC上的动点,现将纸片折叠,使点A与点P重合,折痕与矩形边的交点分别是E,F,要使折痕始终与边AB,AD有交点,则BP的取值范围是( )| A. | $\sqrt{5}≤BP≤5$ | B. | 2≤BP≤6 | C. | $\sqrt{5}≤BP≤6$ | D. | $2≤BP≤5\sqrt{3}$ |
7. 如图,△ABC是⊙O的内接三角形,连接OB、OC.若∠BOC=120°,则∠BAC的度数为( )
如图,△ABC是⊙O的内接三角形,连接OB、OC.若∠BOC=120°,则∠BAC的度数为( )
 如图,△ABC是⊙O的内接三角形,连接OB、OC.若∠BOC=120°,则∠BAC的度数为( )
如图,△ABC是⊙O的内接三角形,连接OB、OC.若∠BOC=120°,则∠BAC的度数为( )| A. | 30° | B. | 45° | C. | 60° | D. | 120° |
1.下列运算中,错误的是( )
| A. | $\frac{x-y}{x+y}$=-$\frac{y-x}{y+x}$ | B. | $\frac{-a-b}{a+b}$=-1 | C. | $\sqrt{{(1-\sqrt{2})}^{2}}$=$\sqrt{2}$-1 | D. | $\sqrt{{a}^{2}}$=a |
5.已知x>y,则-3x+5( )-3y+5,那么括号里应填入( )
| A. | = | B. | > | C. | < | D. | 不能确定 |
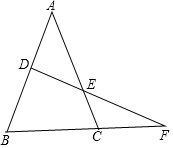 如图,一条直线与△ABC的边AB、AC及BC的延长线交于D、E、F三点,若$\frac{AE}{EC}$=$\frac{BF}{CF}$,请证明点D是AB的中点.
如图,一条直线与△ABC的边AB、AC及BC的延长线交于D、E、F三点,若$\frac{AE}{EC}$=$\frac{BF}{CF}$,请证明点D是AB的中点.