题目内容
6.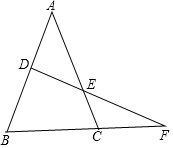 如图,一条直线与△ABC的边AB、AC及BC的延长线交于D、E、F三点,若$\frac{AE}{EC}$=$\frac{BF}{CF}$,请证明点D是AB的中点.
如图,一条直线与△ABC的边AB、AC及BC的延长线交于D、E、F三点,若$\frac{AE}{EC}$=$\frac{BF}{CF}$,请证明点D是AB的中点.
分析 作CK∥DE交AB于K.由DE∥CK,推出$\frac{AE}{EC}$=$\frac{AD}{DK}$,$\frac{BF}{CF}$=$\frac{BD}{DK}$,又因为$\frac{AE}{EC}$=$\frac{BF}{CF}$,即可推出$\frac{AD}{DK}$=$\frac{BD}{DK}$,推出AD=BD.
解答 解:作CK∥DE交AB于K.
∵DE∥CK,
∴$\frac{AE}{EC}$=$\frac{AD}{DK}$,
∵CK∥DF,
∴$\frac{BF}{CF}$=$\frac{BD}{DK}$,
∵$\frac{AE}{EC}$=$\frac{BF}{CF}$,
∴$\frac{AD}{DK}$=$\frac{BD}{DK}$,
∴AD=DB,
∴D是AB中点.
点评 本题考查平行线分线段成比例定理、中点的定义等知识,解题的关键是学会添加常用辅助线,构造平行线解决问题,属于中考常考题型.

练习册系列答案
相关题目
11.MERS属于冠状病毒,病毒粒子成球形,直径约为140纳米(1纳米=0.000000001米),用科学记数法表示为( )
| A. | 1.4×1011米 | B. | 140×109米 | C. | 1.4×10-11米 | D. | 1.4×10-7米 |
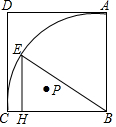 如图,正方形ABCD,以B为圆心,BC长为半径画弧,点E在圆弧上,EH⊥BC于点H,P是△EHB的内心,AB=2,则AP的最小值为$\sqrt{10}$-$\sqrt{2}$.
如图,正方形ABCD,以B为圆心,BC长为半径画弧,点E在圆弧上,EH⊥BC于点H,P是△EHB的内心,AB=2,则AP的最小值为$\sqrt{10}$-$\sqrt{2}$. 如图是某商场2012年至2016年销售额每年比上一年增长率的统计图,则这5年中,该商场销售额最大的是2016年.
如图是某商场2012年至2016年销售额每年比上一年增长率的统计图,则这5年中,该商场销售额最大的是2016年. 如图,BD,CE是△ACB的高,求证:△ADE∽△ABC.
如图,BD,CE是△ACB的高,求证:△ADE∽△ABC.