题目内容
如图，矩形ABCD是由三个矩形拼接成的．如果AB=8，阴影部分的面积是24，另外两个小矩形全等，那么小矩形的长为考点：一元二次方程的应用
专题：几何图形问题
分析：设小矩形的长为x，则小矩形的宽为8-x，然后表示出阴影部分的宽，从而根据其面积列出方程求解即可．
解答：解：设小矩形的长为x，则小矩形的宽为8-x，
根据题意得：x[x-（8-x）]=24，
解得：x=6或x=-2（舍去），
故答案为：6．
根据题意得：x[x-（8-x）]=24，
解得：x=6或x=-2（舍去），
故答案为：6．
点评：考查了一元二次方程的应用，解题的关键是表示出阴影部分的长和宽，难度不大．
练习册系列答案
阅读快车系列答案
相关题目
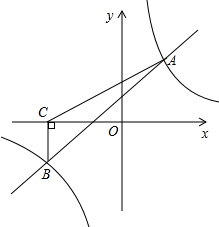如图，一次函数y=kx+b与反比例函数y=
指出下列几何体的截面形状．
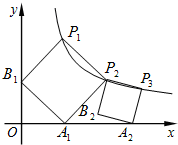正方形的A1B1P1P2顶点P1、P2在反比例函数y=
如图，△ABC与△AEF中，AB=AE，BC=EF，∠B=∠E，AB交EF于D．给出下列结论：