题目内容
在图中,每个图案均由边长为1的小正方形按一定的规律堆叠而成,照此规律,第100个图案中共有 个小正方形.


考点:规律型:图形的变化类
专题:
分析:观察图案不难发现,图案中的正方形按照从上到下成奇数列排布,写出第n个图案的正方形的个数,然后利用求和公式写出表达式,再把n=10代入进行计算即可得解.
解答:解:第1个图案中共有1个小正方形,
第2个图案中共有1+3=4个小正方形,
第3个图案中共有1+3+5=9个小正方形,
…,
第n个图案中共有1+3+5+…+(2n-1)=
=n2个小正方形,
所以,第10个图案中共有1002=10000个小正方形.
故答案为:10000.
第2个图案中共有1+3=4个小正方形,
第3个图案中共有1+3+5=9个小正方形,
…,
第n个图案中共有1+3+5+…+(2n-1)=
| n(1+2n-1) |
| 2 |
所以,第10个图案中共有1002=10000个小正方形.
故答案为:10000.
点评:本题是对图形变化规律的考查,根据图案从上到下的正方形的个数成奇数列排布,得到第n个图案的正方形的个数的表达式是解题的关键.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目
不等式5-x>0的最大整数解是( )
| A、2 | B、3 | C、4 | D、5 |
要使代数式7-3x的值小于-2,则x的取值范围是( )
| A、x>3 | ||
| B、x<3 | ||
| C、x>-3 | ||
D、x>
|
 如图,在△ABC中,∠A:∠C:∠ABC=1:2:3.
如图,在△ABC中,∠A:∠C:∠ABC=1:2:3. 如图,矩形ABCD是由三个矩形拼接成的.如果AB=8,阴影部分的面积是24,另外两个小矩形全等,那么小矩形的长为
如图,矩形ABCD是由三个矩形拼接成的.如果AB=8,阴影部分的面积是24,另外两个小矩形全等,那么小矩形的长为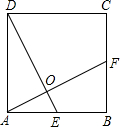 如图,正方形ABCD中,AF⊥DE于点O,tan∠FAB=
如图,正方形ABCD中,AF⊥DE于点O,tan∠FAB= 在△ABC中,tanA=
在△ABC中,tanA=